NCERT Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles - Free PDF
You can now access the premium guide of NCERT Solutions for Class 9 Maths Chapter 9 by Vedantu to prepare thoroughly for your upcoming exam. Now download the CBSE Solutions of Areas of Parallelograms and Triangles PDF to get in-depth knowledge on the core concepts of this chapter. Students can now grab hands on this detailed guide which is curated by experts after extensive research. Make use of essential questions and explanations offered in these guides to revise for your Class 9 exam. Students can also avail of NCERT Solutions for Class 9 Science from our website.
Class: | |
Subject: | |
Chapter Name: | Chapter 9 - Areas of Parallelograms and Triangles |
Content Type: | Text, Videos, Images and PDF Format |
Academic Year: | 2024-25 |
Medium: | English and Hindi |
Available Materials: |
|
Other Materials |
|






Exercises under NCERT Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles
NCERT Solutions for Class 9 Maths Chapter 9 - Areas of Parallelograms and Triangles, has four exercises in total. Each exercise contains different types of questions based on the topics covered in the chapter.
Here are the kinds of questions dealt in each of the four exercises:
Exercise 9.1: This exercise includes basic questions related to the definition of a parallelogram and its properties. Students will learn how to identify and distinguish between different types of parallelograms based on their properties. Questions in this exercise also involve the calculation of the area of a parallelogram using the formula base x height.
Exercise 9.2: This exercise focuses on the properties of triangles, including the types of triangles based on their sides and angles. Students will learn the different ways to calculate the area of a triangle, including the use of Heron's formula. Questions in this exercise also involve finding the area of a given triangle using the Pythagorean theorem.
Exercise 9.3: This exercise involves the calculation of the area of different types of quadrilaterals, including parallelograms, rectangles, squares, and rhombuses. Students will learn how to use the formula for the area of each of these quadrilaterals and also learn the relationship between these shapes.
Exercise 9.4: This exercise contains word problems and real-life examples that require the application of the concepts learned in the previous exercises. Questions in this exercise involve finding the area of a given shape, determining the dimensions of a shape given its area, and solving problems related to the application of these concepts in everyday life.
NCERT Solutions for Class 9 Maths Chapter 9 Areas of Parallelogram and Triangle - PDF Download
EXERCISE 9.1
1. Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
Ans:
Given: Some figures are given.
To find: The figures that lie on the same base and between the same parallels
(i)
Yes. The trapezium ABCD and triangle PCD both have the same base CD and are located between the same parallel lines AB and CD.
(ii)
No. The parallelogram PQRS and the trapezium MNRS have the same basis RS, as can be shown.
However, the vertices of the parallelogram P and Q and the trapezium M and N do not lie on the same line (i.e., opposed to the same base).
(iii)
Yes. The parallelogram PQRS and the triangle TQR share the same base QR and are located between the same parallel lines PS and QR.
(iv)
No. The parallelogram ABCD and the triangle PQR are located between the identical parallel lines AD and BC. These, on the other hand, have no common ground.
(v)
Yes. It can be seen that parallelograms ABCD and APQD have the same base AD and are located between the same parallel lines AD and BQ.
(vi)
No. The parallelograms PBCS and PQRS may be seen resting on the same PS basis. These, on the other hand, do not lay on the same parallel lines.
Exercise (9.2)
1. In the given figure, ABCD is parallelogram, $AE \bot DC{\text{ , }}CF \bot AD$. If AB = 16 cm, AE = 8 cm and CF = 10cm, find AD.
Ans:
Given: ABCD is parallelogram, $AE \bot DC{\text{ , }}CF \bot AD$. If AB = 16 cm, AE = 8 cm and CF = 10cm.
To find: AD.
In parallelogram ABCD, CD = AB = 16 cm
(A parallelogram's opposite sides are equal)
We know that the area of a parallelogram equals the base altitude.
Area of parallelogram $ABCD{\text{ }} = {\text{ }}CD{\text{ }} \times {\text{ }}AE{\text{ }} = {\text{ }}AD{\text{ }} \times {\text{ }}CF$
$16{\text{ }}cm{\text{ }} \times {\text{ }}8{\text{ }}cm{\text{ }} = {\text{ }}AD{\text{ }} \times {\text{ }}10{\text{ }}cm$
$AD = \dfrac{{16(8)}}{{10}}cm = 12.8cm$
Hence, the length of AD is 12.8 cm.
2. If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD show that $\;ar{\text{ }}\left( {EFGH} \right){\text{ }} = {\text{ }}\dfrac{1}{2}ar{\text{ }}\left( {ABCD} \right)$
Ans:
Given: E, F, G, and H are the mid-points of the sides of a parallelogram ABCD
To prove: $\;ar{\text{ }}\left( {EFGH} \right){\text{ }} = {\text{ }}\dfrac{1}{2}ar{\text{ }}\left( {ABCD} \right)$
Let us join HF.
In parallelogram ABCD,
AD = BC and $AD{\text{ }}||{\text{ }}BC$ (Opposite sides of a parallelogram are equal and parallel)
AB = CD (Opposite sides of a parallelogram are equal)
$\dfrac{1}{2}AD{\text{ = }}\dfrac{1}{2}BC{\text{ }}$and $AH{\text{ }}||{\text{ }}BF$
⇒ AH = BF and $AH{\text{ }}||{\text{ }}BF$(H and F are the mid-points of AD and BC)
So, ABFH is a parallelogram.
Since $\Delta HEF$ and parallelogram ABFH are on same base HF and between same parallels AB and HF,
$\therefore $ Area $(\Delta {\text{HEF}}) = \dfrac{1}{2}$ Area (ABFH)$ \ldots (1)$
We know that, it can be proved that
Area $(\Delta {\text{HGF}}) = \dfrac{1}{2}$ Area (HDCF)
On adding Equations (1) and (2), we obtain
Area $(\vartriangle {\text{HEF}}) + $ Area $(\Delta {\text{HGF}}) = \dfrac{1}{2}$ Area $({\text{ABFH}}) + \dfrac{1}{2}$ Area $({\text{HDCF}})$
$ = \dfrac{1}{2}[$ Area $({\text{ABFH}}) + $ Area $({\text{HDCF}})]$
$ \Rightarrow $ Area $({\text{EFGH}}) = \dfrac{1}{2}$ Area $({\text{ABCD}})$
3. P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that $ar{\text{ }}\left( {APB} \right){\text{ }} = {\text{ }}ar{\text{ }}(BQC)$.
Ans:
Given: P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD.
To prove: $ar{\text{ }}\left( {APB} \right){\text{ }} = {\text{ }}ar{\text{ }}(BQC)$.
It can be observed that $\Delta BQC$ and parallelogram ABCD lie on same base BC and these are between same parallel lines AD and BC.
$\therefore Area{\text{ }}\left( {\Delta BQC} \right){\text{ }} = {\text{ }}\dfrac{1}{2}Area{\text{ }}\left( {ABCD} \right){\text{ }}...{\text{ }}\left( 1 \right)$
We know that, $\Delta APB$ and parallelogram ABCD lie on the same base AB and between the same parallel lines AB and DC.
$\therefore Area{\text{ }}\left( {\Delta APB} \right){\text{ }} = {\text{ }}\dfrac{1}{2}Area{\text{ }}\left( {ABCD} \right){\text{ }}...{\text{ }}\left( 2 \right)$
Upon (1) and (2, we obtain
$Area{\text{ }}\left( {\Delta BQC} \right){\text{ }} = {\text{ }}Area{\text{ }}\left( {\Delta APB} \right)$
4. In the given figure, P is a point in the interior of a parallelogram ABCD. Show that
(i) $ar{\text{ }}\left( {APB} \right){\text{ }} + {\text{ }}ar{\text{ }}\left( {PCD} \right){\text{ }} = {\text{ }}\dfrac{1}{2}ar{\text{ }}\left( {ABCD} \right)$
(ii) $ar{\text{ }}\left( {APD} \right){\text{ }} + {\text{ }}ar{\text{ }}\left( {PBC} \right){\text{ }} = {\text{ }}ar{\text{ }}\left( {APB} \right){\text{ }} + {\text{ }}ar{\text{ }}\left( {PCD} \right)$
(Hint: Through P, draw a line parallel to AB)
Ans:
Given: P is a point in the interior of a parallelogram ABCD
To prove: (i) $ar{\text{ }}\left( {APB} \right){\text{ }} + {\text{ }}ar{\text{ }}\left( {PCD} \right){\text{ }} = {\text{ }}\dfrac{1}{2}ar{\text{ }}\left( {ABCD} \right)$
(ii) $ar{\text{ }}\left( {APD} \right){\text{ }} + {\text{ }}ar{\text{ }}\left( {PBC} \right){\text{ }} = {\text{ }}ar{\text{ }}\left( {APB} \right){\text{ }} + {\text{ }}ar{\text{ }}\left( {PCD} \right)$
(i) Let us draw a line segment EF, passing through point P and parallel to line segment AB.
In parallelogram ABCD,
$AB{\text{ }}||{\text{ }}EF$ (By construction) ... (1)
ABCD is a parallelogram.
$\therefore AD{\text{ }}||{\text{ }}BC$ (Opposite sides of a parallelogram)
$ \Rightarrow AE{\text{ }}||{\text{ }}BF$... (2)
Upon (1) and (2, we obtain $AB{\text{ }}\left| {\left| {{\text{ }}EF{\text{ , }}AE{\text{ }}} \right|} \right|{\text{ }}BF$
So, quadrilateral ABFE is a parallelogram.
It can be observed that $\Delta APB$ and parallelogram ABFE are lying on same base AB and between same parallel lines AB and EF.
$\therefore Area\left( {\Delta APB} \right){\text{ }} = {\text{ }}\dfrac{1}{2}Area{\text{ }}\left( {ABFE} \right){\text{ }}...{\text{ }}\left( 3 \right)$
We know that, for ∆PCD and parallelogram EFCD,
$Area{\text{ }}\left( {\Delta PCD} \right){\text{ }} = {\text{ }}\dfrac{1}{2}{\text{ }}Area{\text{ }}\left( {EFCD} \right){\text{ }}...{\text{ }}\left( 4 \right)$
Adding Equations (3) and (4), we obtain
$Area{\text{ }}\left( {\Delta APB} \right){\text{ }} + {\text{ }}Area{\text{ }}\left( {\Delta PCD} \right){\text{ }} = {\text{ }}\dfrac{1}{2}\left[ {Area{\text{ }}\left( {ABFE} \right){\text{ }} + {\text{ }}Area{\text{ }}\left( {EFCD} \right)} \right]$
$Area{\text{ }}\left( {\Delta APB} \right){\text{ }} + {\text{ }}Area{\text{ }}\left( {\Delta PCD} \right){\text{ }} = {\text{ }}\dfrac{1}{2}{\text{ }}Area{\text{ }}\left( {ABCD} \right){\text{ }}...{\text{ }}\left( 5 \right)$
(ii) Let us draw a line segment MN, passing through point P and parallel to line segment AD. In parallelogram ABCD,
$MN{\text{ }}||{\text{ }}AD$ (By construction) ... (6)
ABCD is a parallelogram.
$\therefore AB{\text{ }}||{\text{ }}DC$ (Opposite sides of a parallelogram)
$ \Rightarrow AM{\text{ }}||{\text{ }}DN{\text{ }}...{\text{ }}\left( 7 \right)$
From Equations (6) and (7), we obtain
$MN{\text{ }}\left| {\left| {{\text{ }}AD{\text{ , }}AM{\text{ }}} \right|} \right|{\text{ }}DN$
So, quadrilateral AMND is a parallelogram.
It can be observed that $\Delta APD$ and parallelogram AMND are lying on the same base AD and between the same parallel lines AD and MN.
$\therefore Area{\text{ }}\left( {\Delta APD} \right){\text{ }} = {\text{ }}12Area{\text{ }}\left( {AMND} \right){\text{ }}...{\text{ }}\left( 8 \right)$
We know that, for ∆PCB and parallelogram MNCB,
$Area{\text{ }}\left( {\Delta PCB} \right){\text{ }} = {\text{ }}\dfrac{1}{2}Area{\text{ }}\left( {MNCB} \right){\text{ }}...{\text{ }}\left( 9 \right)$
Adding Equations (8) and (9), we obtain
$Area{\text{ }}\left( {\Delta APD} \right){\text{ }} + {\text{ }}Area{\text{ }}\left( {\Delta PCB} \right){\text{ }} = {\text{ }}\dfrac{1}{2}\left[ {Area{\text{ }}\left( {AMND} \right){\text{ }} + {\text{ }}Area{\text{ }}\left( {MNCB} \right)} \right]$
$Area{\text{ }}\left( {\Delta APD} \right){\text{ }} + {\text{ }}Area{\text{ }}\left( {\Delta PCB} \right){\text{ }} = {\text{ }}\dfrac{1}{2}Area{\text{ }}\left( {ABCD} \right){\text{ }}...{\text{ }}\left( {10} \right)$
upon comparing Equations (5) and (10), we obtain
$Area{\text{ }}\left( {\Delta APD} \right){\text{ }} + {\text{ }}Area{\text{ }}\left( {\Delta PBC} \right){\text{ }} = {\text{ }}Area{\text{ }}\left( {\Delta APB} \right){\text{ }} + {\text{ }}Area{\text{ }}\left( {\Delta PCD} \right)$
5. In the given figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that
(i) ar (PQRS) = ar (ABRS)
(ii) $ar{\text{ }}\left( {\Delta PXS} \right){\text{ }} = {\text{ }}\dfrac{1}{2}ar{\text{ }}\left( {PQRS} \right)$
Ans:
Given: PQRS and ABRS are parallelograms and X is any point on side BR.
To prove: (i) ar (PQRS) = ar (ABRS)
(ii) $ar{\text{ }}\left( {\Delta PXS} \right){\text{ }} = {\text{ }}\dfrac{1}{2}ar{\text{ }}\left( {PQRS} \right)$
(i) It can be observed that parallelogram PQRS and ABRS lie upon same base SR and also, these lie in between same parallel lines SR and PB.
$\therefore Area{\text{ }}\left( {PQRS} \right){\text{ }} = {\text{ }}Area{\text{ }}\left( {ABRS} \right){\text{ }}...{\text{ }}\left( 1 \right)$
(ii) Consider $\Delta AXS$and parallelogram ABRS.
As these lie on the same base and are between the same parallel lines AS and BR,
$\therefore Area{\text{ }}\left( {\Delta AXS} \right){\text{ }} = {\text{ }}\dfrac{1}{2}{\text{ }}Area{\text{ }}\left( {ABRS} \right){\text{ }}...{\text{ }}\left( 2 \right)$
Upon (1) and (2, we obtain
$Area\left( {\Delta AXS} \right){\text{ }} = {\text{ }}\dfrac{1}{2}Area{\text{ }}\left( {PQRS} \right)$
6. A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the field is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?
Ans:
Given: A farmer had a field that was shaped like a parallelogram PQRS. She connected any point A on RS with points P and Q.
To find: How many pieces does the field have? What are the dimensions of these components? The farmer intends to sow wheat and pulses separately in equal parts of the land. What is the best way for her to go about it?
From the figure, it can be observed that point A divides the field into three parts.
These parts are triangular in shape − $\Delta PSA,{\text{ }}\Delta PAQ,{\text{ }}\Delta QRA$
Area of $\Delta PSA$ + Area of ${\text{ }}\Delta PAQ$ + Area of ${\text{ }}\Delta QRA$ = Area of parallelogram PQRS ... (1)
We know that if that parallelogram and a triangle are on same base and between the same parallels, then the area of the triangle is half the area of the given parallelogram.
$\therefore Area{\text{ }}\left( {\Delta PAQ} \right){\text{ }} = {\text{ }}\dfrac{1}{2}{\text{ }}Area{\text{ }}\left( {PQRS} \right){\text{ }}...{\text{ }}\left( 2 \right)$
Upon (1) and (2, we obtain
$Area{\text{ }}\left( {\Delta PSA} \right){\text{ }} + {\text{ }}Area{\text{ }}\left( {\Delta QRA} \right){\text{ }} = {\text{ }}\dfrac{1}{2}{\text{ }}Area{\text{ }}\left( {PQRS} \right){\text{ }}...{\text{ }}\left( 3 \right)$
It is clear that the farmer must seed wheat in the PAQ triangle portion and pulses in the PSA and QRA triangular parts, or wheat in the PSA and QRA triangular parts and pulses in the PAQ triangular parts.
Exercise 9.3
1. In the given figure, E is any point on median AD of a $\Delta ABC$. Show that ar (ABE) = ar (ACE)
Ans:
Given: E is any point on median AD of a $\Delta ABC$.
To prove: ar (ABE) = ar (ACE)
AD is the median of $\vartriangle ABC$. So, it will divide $\vartriangle ABC$ into two triangles of equal areas.
$\therefore $ Area $(\vartriangle {\text{ABD}}) = $ Area $(\vartriangle {\text{ACD}}) \ldots $ (1)
ED is the median of $\Delta EBC$.
$\therefore $ Area $(\Delta {\text{EBD}}) = $ Area $(\Delta {\text{ECD}}) \ldots (2)$
On subtracting Equation (2) from Equation (1), we obtain
Area $(\vartriangle {\text{ABD}}) - $ Area $({\text{EBD}}) = $ Area $(\vartriangle {\text{ACD}}) - $ Area $(\Delta {\text{ECD}})$
Area $(\vartriangle {\text{ABE}}) = $ Area $(\vartriangle {\text{ACE}})$
2. In a triangle ${\text{ABC}},{\text{E}}$ is the mid-point of median ${\text{AD}}$. Show that $\operatorname{ar} (\Delta {\text{BED}}) = \dfrac{1}{4}\operatorname{ar} (\vartriangle {\text{ABC}})$
Ans:
Given: A $\vartriangle ABC,AD$ is the median and $E$ is the mid-point of median AD.
To prove: $\operatorname{ar} (\Delta {\text{BED}}) = \dfrac{1}{4}\operatorname{ar} (\vartriangle {\text{ABC}})$
To prove: $\operatorname{ar} (\Delta {\text{BED}}) = 1/4\operatorname{ar} (\Delta {\text{ABC}})$
Proof : In $\vartriangle {\text{ABC}},{\text{AD}}$ is the median.
$\therefore $ ar $(\Delta {\text{ABD}}) = \operatorname{ar} (\Delta {\text{ADC}})$
$[\therefore $ Median divides a $\Delta $ into two $\Delta $ s of equal area $]$
$\operatorname{ar} (\Delta {\text{ABD}}) = \dfrac{1}{2}\operatorname{ar} ({\text{ABC}})$
In $\vartriangle {\text{ABD}},{\text{BE}}$ is the median.
$\operatorname{ar} (\Delta {\text{BED}}) = \operatorname{ar} (\Delta {\text{BAE}})$
$\therefore $ ar $(\Delta {\text{BED}}) = \dfrac{1}{2}\operatorname{ar} (\Delta {\text{ABD}})$
$ = \operatorname{ar} (\Delta {\text{BED}}) = \dfrac{1}{2}\left[ {\dfrac{1}{2}\operatorname{ar} (\Delta {\text{ABC}})} \right] = \dfrac{1}{2}\operatorname{ar} (\Delta {\text{ABC}})$
3. how that the diagonals of a parallelogram divide it into four triangles of equal area.
Ans:
Given: Diagonals of a parallelogram.
To prove: Diagonals of a parallelogram divide it into four triangles of equal area.
We know that diagonals of parallelograms bisect each other.
So, O is the mid-point of AC and BD.
BO is the median in $\Delta ABC$. So, it will divide it into two triangles of equal areas.
$\therefore Area{\text{ }}\left( {\Delta AOB} \right){\text{ }} = {\text{ }}Area{\text{ }}\left( {\Delta BOC} \right){\text{ }}...{\text{ }}\left( 1 \right)$
In $\Delta BCD$, CO is the median.
$\therefore Area{\text{ }}\left( {\Delta BOC} \right){\text{ }} = {\text{ }}Area{\text{ }}\left( {\Delta COD} \right){\text{ }}...{\text{ }}\left( 2 \right)$
We know that, $Area{\text{ }}\left( {\Delta COD} \right){\text{ }} = {\text{ }}Area\left( {\Delta AOD} \right)$... (3)
From Equations (1), (2), and (3), we obtain
$Area{\text{ }}\left( {\Delta AOB} \right){\text{ }} = {\text{ }}Area{\text{ }}\left( {\Delta BOC} \right){\text{ }} = {\text{ }}Area{\text{ }}\left( {\Delta COD} \right){\text{ }} = {\text{ }}Area{\text{ }}\left( {\Delta AOD} \right)$
So, it is evident that diagonals of a parallelogram divide it into 4 triangles of equal area.
4. In the given figure, ABC and ABD are two triangles on the same base AB. If line-segment CD is bisected by AB at O, show that ar (ABC) = ar (ABD).
Ans:
Given: ABC and ABD are two triangles on the same base AB. If the line-segment CD is bisected by AB at O.
To prove: ar (ABC) = ar (ABD).
Consider $\Delta ACD$.
Line-segment CD is bisected by AB at O. So, AO is the median of $\Delta ACD$.
$\therefore Area\left( {\Delta ACO} \right){\text{ }} = {\text{ }}Area\left( {\Delta ADO} \right){\text{ }}...{\text{ }}\left( 1 \right)$
Considering $\Delta BCD$, BO is the median.
$\therefore Area{\text{ }}\left( {\Delta BCO} \right){\text{ }} = {\text{ }}Area{\text{ }}\left( {\Delta BDO} \right){\text{ }}...{\text{ }}\left( 2 \right)$
Adding Equations (1) and (2), we obtain
$Area{\text{ }}\left( {\Delta ACO} \right){\text{ }} + {\text{ }}Area{\text{ }}\left( {\Delta BCO} \right){\text{ }} = {\text{ }}Area{\text{ }}\left( {\Delta ADO} \right){\text{ }} + {\text{ }}Area{\text{ }}\left( {\Delta BDO} \right)$
$ \Rightarrow Area{\text{ }}\left( {\Delta ABC} \right){\text{ }} = {\text{ }}Area{\text{ }}\left( {\Delta ABD} \right)$
5. D, E and F are respectively the mid-points of the sides BC, CA and AB of a $\Delta ABC$. Show that:
(i) BDEF is a parallelogram.
(ii) $ar{\text{ }}\left( {DEF} \right){\text{ }} = {\text{ }}\dfrac{1}{4}ar{\text{ }}\left( {ABC} \right)$
(iii) $ar{\text{ }}\left( {BDEF} \right){\text{ }} = {\text{ }}\dfrac{1}{2}{\text{ }}ar{\text{ }}\left( {ABC} \right)$
Ans:
Given: D, E and F are respectively the mid-points of the sides BC, CA and AB of a $\Delta ABC$. To prove:
(i) BDEF is a parallelogram.
(ii) $ar{\text{ }}\left( {DEF} \right){\text{ }} = {\text{ }}\dfrac{1}{4}ar{\text{ }}\left( {ABC} \right)$
(iii) $ar{\text{ }}\left( {BDEF} \right){\text{ }} = {\text{ }}\dfrac{1}{2}{\text{ }}ar{\text{ }}\left( {ABC} \right)$
(i) F is the mid-point of AB and E is the mid-point of AC.
and $FE{\text{ }} = \dfrac{1}{2}{\text{ }}BD$
Line joining the mid-points of two sides of a triangle is parallel to the third and half of It
(BD is the part of BC)
And FE = BD
Also, D is the mid-point of BC.
$\therefore BD{\text{ }} = {\text{ }}\dfrac{1}{2}{\text{ }}BC$
And and FE = BD
Again ${\text{E}}$ is the mid-point of ${\text{AC}}$ and ${\text{D}}$ is the mid-point of ${\text{BC}}$. and ${\text{DE}} = \dfrac{1}{2}{\text{AB}}$
is the part of ${\text{AB}}]$
And ${\text{DE}} = {\text{BF}}$
Again ${\text{F}}$ is the mid-point of ${\text{AB}}$.
$\therefore {\text{BF}} = \dfrac{1}{2}{\text{AB}}$
But ${\text{DE}} = \dfrac{1}{2}{\text{AB}}$
$\therefore {\text{DE}} = {\text{BF}}$
Now we have and
And ${\text{FE}} = {\text{BD}}$ and ${\text{DE}} = {\text{BF}}$
Therefore, BDEF is a parallelogram
(ii) ${\text{BDEF}}$ is a parallelogram.
$\therefore \operatorname{ar} (\Delta {\text{BDF}}) = \operatorname{ar} (\Delta {\text{DEF}})$
diagonals of parallelogram divides it in two triangles of equal area] DCEF is also parallelogram.
$\therefore $ ar $(\Delta {\text{DEF}}) = \operatorname{ar} (\vartriangle {\text{DEC}}) \ldots \ldots \ldots $ (ii)
Also, AEDF is also parallelogram. $\therefore $ ar $(\Delta {\text{AFE}}) = \operatorname{ar} (\Delta {\text{DEF}}) \ldots \ldots \ldots \ldots $ (iii)
From eq. (i), (ii) and (iii),
$\operatorname{ar} (\vartriangle {\text{DEF}}) = \operatorname{ar} (\Delta {\text{BDF}}) = \operatorname{ar} (\vartriangle {\text{DEC}}) = \operatorname{ar} (\vartriangle {\text{AFE}}) \ldots \ldots \ldots .$ (iv)
Now, ar $(\vartriangle {\text{ABC}}) = \operatorname{ar} (\vartriangle {\text{DEF}}) + \operatorname{ar} (\vartriangle {\text{BDF}}) + \operatorname{ar} (\vartriangle {\text{DEC}}) + \operatorname{ar} (\Delta {\text{AFE}}) \ldots \ldots \ldots ..({\text{v}})$
$\operatorname{ar} (\vartriangle {\text{ABC}}) = \operatorname{ar} (\Delta {\text{DEF}}) + \operatorname{ar} (\vartriangle {\text{DEF}}) + \operatorname{ar} (\Delta {\text{DEF}}) + \operatorname{ar} (\Delta {\text{DEF}})$
(Using (iv) & (v))
$\operatorname{ar} (\vartriangle {\text{ABC}}) = 4 \times \operatorname{ar} ({\text{ADEF}})$
$\operatorname{ar} (\Delta {\text{DEF}}) = \dfrac{1}{4}$ ar $(\vartriangle {\text{ABC}})$
(iii) ar [Using (iv)]
ar $(\Delta DEF)$
6. In the given figure, diagonals ${\text{AC}}$ and ${\text{BD}}$ of quadrilateral ${\text{ABCD}}$ intersect at ${\text{O}}$ such that ${\text{OB}} = $ OD. If $AB = CD$, then show that:
(i) ar $({\text{DOC}}) = \operatorname{ar} ({\text{AOB}})$
(ii) ar $({\text{DCB}}) = $ ar $({\text{ACB}})$
(iii) or ${\text{ABCD}}$ is a parallelogram
(Hint: From D and B, draw perpendiculars to AC.)
Ans:
Given: In the given figure, diagonals ${\text{AC}}$ and ${\text{BD}}$ of quadrilateral ${\text{ABCD}}$ intersect at ${\text{O}}$ such that ${\text{OB}} = $ OD. If $AB = CD$
To prove: (i) ar $({\text{DOC}}) = \operatorname{ar} ({\text{AOB}})$
(ii) ar $({\text{DCB}}) = $ ar $({\text{ACB}})$
(iii) or ${\text{ABCD}}$ is a parallelogram
Let us draw ${\text{DN}} \bot {\text{AC}}$ and ${\text{BM}} \bot {\text{AC}}$.
(i) In $\vartriangle {\text{DON}}$ and $\vartriangle {\text{BOM}}$,
$\angle {\text{DNO}} = \angle {\text{BMO}}$ (By construction)
$\angle {\text{DON}} = \angle {\text{BOM}}($ Vertically opposite angles $)$ ${\text{OD}} = {\text{OB}}$ (Given)
By AAS congruence rule,
$\vartriangle {\text{DON}} \cong \vartriangle {\text{BOM}}$
${\text{DN}} = {\text{BM}}$
We know that congruent triangles have equal areas. Area $(\vartriangle {\text{DON}}) = $ Area $(\vartriangle {\text{BOM}})\quad \ldots $
In $\vartriangle {\text{DNC}}$ and $\vartriangle {\text{BMA}}$,
$\angle {\text{DNC}} = \angle {\text{BMA}}$ (By construction)
${\text{CD}} = {\text{AB}}$ (given)
${\text{DN}} = {\text{BM}}[$ Using Equation (1)]
$\therefore \vartriangle {\text{DNC}} \cong \vartriangle {\text{BMA}}$ (RHS congruence rule)
$\therefore $ Area $(\vartriangle {\text{DNC}}) = $ Area $(\Delta {\text{BMA}})$$ \ldots $ (3)
On adding Equations (2) and (3), we obtain
Area ( $(\vartriangle {\text{DON}}) + $ Area $(\Delta {\text{DNC}}) = $ Area $(\vartriangle {\text{BOM}}) + $ Area ( $\vartriangle {\text{BMA}})$
Therefore, Area $(\vartriangle {\text{DOC}}) = $ Area $(\vartriangle {\text{AOB}})$
(ii) We obtained, Area $(\Delta {\text{DOC}}) = $ Area $(\vartriangle {\text{AOB}})$
$\therefore $ Area $(\vartriangle {\text{DOC}}) + $ Area $(\Delta {\text{OCB}}) = $ Area $(\vartriangle {\text{AOB}}) + $ Area $(\Delta {\text{OCB}})$
(Adding Area $(\Delta OCB)$ to both sides)
$\therefore $ Area $(\vartriangle {\text{DCB}}) = $ Area $(\vartriangle {\text{ACB}})$
(iii) We obtained, Area $(\Delta {\text{DCB}}) = $ Area $(\vartriangle {\text{ACB}})$
If two triangles have the same base and equal areas, then these will lie between the same parallels.
$ \ldots $ (4)
In quadrilateral ${\text{ABCD}}$, one pair of opposite sides is equal $({\text{AB}} = {\text{CD}})$ and the other pair of opposite sides is parallel (DA ).
Therefore, ${\text{ABCD}}$ is a parallelogram
7. ${\text{D}}$ and ${\text{E}}$ are points on sides ${\text{AB}}$ and ${\text{AC}}$ respectively of $\vartriangle {\text{ABC}}$ such that ar $({\text{DBC}}) = $ ar $({\text{EBC}})$. Prove that .
Ans:
Given: ${\text{D}}$ and ${\text{E}}$ are points on sides ${\text{AB}}$ and ${\text{AC}}$ respectively of $\vartriangle {\text{ABC}}$ such that ar $({\text{DBC}}) = $ ar $({\text{EBC}})$.
To Prove: .
Since $\vartriangle {\text{BCE}}$ and $\vartriangle {\text{BCD}}$ are lying on a common base ${\text{BC}}$ and also have equal areas, $\vartriangle {\text{BCE}}$ and
$\vartriangle {\text{BCD}}$ will lie between the same parallel lines.
8. ${\text{XY}}$ is a line parallel to side ${\text{BC}}$ of a triangle ${\text{ABC}}$. If and meet ${\text{XY}}$ at ${\text{E}}$ and ${\text{F}}$ respectively, show that ar $(ABE) = $ ar $(ACF)$
Ans:
Given: ${\text{XY}}$ is a line parallel to side ${\text{BC}}$ of a triangle ${\text{ABC}}$. If and meet ${\text{XY}}$ at ${\text{E}}$ and ${\text{F}}$ respectively.
To prove: ar $(ABE) = $ ar $(ACF)$
Parallelograms EBCY and BCFX are on the same base ${\text{BC}}$ and between the same parallels ${\text{BC}}$ and ${\text{EF}}$.
$\therefore $ Area $({\text{EBCY}}) = \dfrac{1}{2}$ Area $({\text{BCFX}})\quad \ldots $
Consider parallelogram EBCY and $\vartriangle $ AEB These lie on the same base ${\text{BE}}$ and are between the same parallels ${\text{BE}}$ and ${\text{AC}}$.
(2)
$\therefore $ Area $(\vartriangle {\text{ABE}}) = \dfrac{1}{2}$ Area (EBCY) $ \ldots $
Also, parallelogram $\Delta {\text{CFX}}$ and $\vartriangle {\text{ACF}}$ are on the same base ${\text{CF}}$ and between the same parallels
${\text{CF}}$ and ${\text{AB}}$.
$\therefore $ Area $(\Delta {\text{ACF}}) = \dfrac{1}{2}$ Area $({\text{BCFX}})\quad \ldots (3)$
From Equations (1), (2), and (3), we obtain Area $(\vartriangle {\text{ABE}}) = $ Area $(\vartriangle {\text{ACF}})$
9. The side ${\text{AB}}$ of a parallelogram ${\text{ABCD}}$ is produced to any point ${\text{P}}$. A line through ${\text{A}}$ and parallel to CP meets CB produced at $Q$ and then parallelogram PBQR is completed (see the following figure). Show that ar $({\text{ABCD}}) = $ ar (PBQR).
(Hint. Join ${\text{AC}}$ and ${\text{PQ}}$. Now compare area ( ${\text{ACQ}}$ ) and area (APQ))
Ans:
Given: The side ${\text{AB}}$ of a parallelogram ${\text{ABCD}}$ is produced to any point ${\text{P}}$. A line through ${\text{A}}$ and parallel to CP meets CB produced at $Q$ and then parallelogram PBQR is completed.
To prove: ar $({\text{ABCD}}) = $ ar (PBQR).
Let us join ${\text{AC}}$ and ${\text{PQ}}$.
$\vartriangle {\text{ACQ}}$ and $\vartriangle {\text{AQP}}$ are on the same base ${\text{AQ}}$ and between the same parallels ${\text{AQ}}$ and ${\text{CP}}$.
Area $(\vartriangle {\text{ACQ}}) = $ Area $(\vartriangle {\text{APQ}})$
Area $(\Delta {\text{ACQ}}) - $ Area $(\vartriangle {\text{ABQ}}) = $ Area $(\vartriangle {\text{APQ}}) - $ Area $(\vartriangle {\text{ABQ}})$
Area $(\vartriangle {\text{ABC}}) = $ Area $(\Delta {\text{QBP}})$
Since ${\text{AC}}$ and ${\text{PQ}}$ are diagonals of parallelograms ${\text{ABCD}}$ and PBQR respectively, Area $(\vartriangle {\text{ABC}}) = \dfrac{1}{2}$ Area $({\text{ABCD}})$
Area $(\Delta {\text{QBP}}) = \dfrac{1}{2}$ Area $({\text{PBQR}})$
From Equations (1), (2), and (3), we obtain $\dfrac{1}{2}$ Area $({\text{ABCD}}) = \dfrac{1}{2}$ Area (PBQR)
Area $({\text{ABCD}}) = $ Area (PBQR)
10. Diagonals ${\text{AC}}$ and ${\text{BD}}$ of a trapezium ${\text{ABCD}}$ with intersect each other at ${\text{O}}$. Prove that ar $({\text{AOD}}) = \operatorname{ar} ({\text{BOC}})$.
Ans:
Given: Diagonals ${\text{AC}}$ and ${\text{BD}}$ of a trapezium ${\text{ABCD}}$ with intersect each other at ${\text{O}}$.
To Prove: ar $({\text{AOD}}) = \operatorname{ar} ({\text{BOC}})$.
It can be observed that $\vartriangle {\text{DAC}}$ and $\vartriangle {\text{DBC}}$ lie on the same base ${\text{DC}}$ and between the same parallels ${\text{AB}}$ and ${\text{CD}}$.
Area $(\vartriangle {\text{DAC}}) = $ Area $(\vartriangle {\text{DBC}})$
Area $(\Delta {\text{DAC}}) - $ Area $(\vartriangle {\text{DOC}}) = $ Area $(\vartriangle {\text{DBC}}) - $ Area $(\vartriangle {\text{DOC}})$
Area $(\vartriangle {\text{AOD}}) = $ Area $(\vartriangle {\text{BOC}})$
11. In the given figure, ${\text{ABCDE}}$ is a pentagon ${\text{A}}$ line through B parallel to ${\text{AC}}$ meets ${\text{DC}}$ produced at $F$. Show that
(i) ar $({\text{ACB}}) = \operatorname{ar} ({\text{ACF}})$
(ii) ar $({\text{AEDF}}) = $ ar $({\text{ABCDE}})$
Ans:
Given: ${\text{ABCDE}}$ is a pentagon ${\text{A}}$ line through B parallel to ${\text{AC}}$ meets ${\text{DC}}$ produced at $F$.
To prove:
(i) ar $({\text{ACB}}) = \operatorname{ar} ({\text{ACF}})$
(ii) ar $({\text{AEDF}}) = $ ar $({\text{ABCDE}})$
(i) $\Delta ACB$ and $\Delta ACF$lie on the same base AC and are between
The same parallels AC and BF.
Area ($\Delta ACB$) = Area ($\Delta ACF$)
(ii) It can be observed that
Area ($\Delta ACB$) = Area ($\Delta ACF$)
Area ($\Delta ACB$) + Area (ACDE) = Area ($\Delta ACF$) + Area (ACDE)
Area (ABCDE) = Area (AEDF)
12. A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given an equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Ans:
Given: Itwaari, a peasant, owns a quadrilateral-shaped parcel of land. The village's Gram Panchayat decided to take over a piece of his property on one of the corners to build a health center. Itwaari agrees to the aforementioned proposition on the condition that he be given an equal amount of land in exchange for the property adjacent to his allotment, forming a triangle plot.
To prove: Describe how this suggestion will be put into action.
Let quadrilateral ABCD be the original shape of the field.
The proposal may be implemented as follows.
Join diagonal BD and draw a line parallel to BD through point A.
Let it meet the extended side CD of ABCD at point E.
Join BE and AD. Let them intersect each other at O.
Then, portion $\Delta AOB$can be cut from the original field so that the new shape of the field will be $\Delta BCE$. (See figure).
We have to prove that the area of ∆AOB (the portion that was cut so as to construct the Health Centre)
is equal to the area of ∆DEO (portion added to the field so as to make the area of the new field so formed equal to the area of the original field).
It can be observed that $\vartriangle {\text{DEB}}$ and $\vartriangle {\text{DAB}}$ lie on the same base ${\text{BD}}$ and are between the same parallels BD and ${\text{AE}}$.
Area $(\Delta {\text{DEB}}) = $ Area $(\vartriangle {\text{DAB}})$
Area $(\Delta {\text{DEB}}) - $ Area $(\vartriangle {\text{DOB}}) = $ Area $(\vartriangle {\text{DAB}}) - $ Area $(\vartriangle {\text{DOB}})$
Area $(\Delta {\text{DEO}}) = $ Area $(\vartriangle {\text{AOB}})$
13. ${\text{ABCD}}$ is a trapezium with . A line parallel to ${\text{AC}}$ intersects ${\text{AB}}$ at ${\text{X}}$ and ${\text{BC}}$ at ${\text{Y}}$. Prove that ar $({\text{ADX}}) = \operatorname{ar} ({\text{ACY}})$. [Hint: Join CX.]
Ans:
Given: ${\text{ABCD}}$ is a trapezium with . A line parallel to ${\text{AC}}$ intersects ${\text{AB}}$ at ${\text{X}}$ and ${\text{BC}}$ at ${\text{Y}}$.
To Prove: ar $({\text{ADX}}) = \operatorname{ar} ({\text{ACY}})$.
It can be observed that $\vartriangle {\text{ADX}}$ and $\vartriangle {\text{ACX}}$ lie on the same base ${\text{AX}}$ and are between the same parallels ${\text{AB}}$ and ${\text{DC}}$.
Area $(\vartriangle {\text{ADX}}) = $ Area $(\vartriangle {\text{ACX}})$
$\vartriangle {\text{ACY}}$ and $\vartriangle {\text{ACX}}$ lie on the same base ${\text{AC}}$ and are between the same parallels ${\text{AC}}$ and ${\text{XY}}$.
Area $(\vartriangle {\text{ACY}}) = $ Area $({\text{ACX}})$
Upon (1) and (2, we obtain
Area $(\Delta {\text{ADX}}) = $ Area $(\vartriangle {\text{ACY}})$
14. In the given figure, Prove that ar $({\text{AQC}}) = {\text{ar}}({\text{PBR}})$.
Ans:
Given:
To prove: ar $({\text{AQC}}) = {\text{ar}}({\text{PBR}})$
Since $\vartriangle {\text{ABQ}}$ and $\vartriangle {\text{PBQ}}$ lie on the same base ${\text{BQ}}$ and are between the same parallels ${\text{AP}}$ and ${\text{BQ}}$,
$\therefore $ Area $(\vartriangle {\text{ABQ}}) = $ Area $(\Delta {\text{PBQ}})$ $ \ldots $ (1)
Again, $\vartriangle {\text{BCQ}}$ and $\vartriangle {\text{BRQ}}$ lie on the same base ${\text{BQ}}$ and are between the same parallels ${\text{BQ}}$ and CR.
$\therefore $ Area $(\Delta {\text{BCQ}}) = $ Area $(\vartriangle {\text{BRQ}})\quad \ldots (2)$
On adding Equations (1) and (2), we obtain
Area $(\Delta {\text{ABQ}}) + $ Area $(\vartriangle {\text{BCQ}}) = $ Area $(\Delta {\text{PBQ}}) + $ Area $(\vartriangle {\text{BRQ}})$
$\therefore $ Area $(\vartriangle {\text{AQC}}) = $ Area ( $\vartriangle {\text{PBR}})$
15. Diagonals ${\text{AC}}$ and ${\text{BD}}$ of a quadrilateral ${\text{ABCD}}$ intersect at ${\text{O}}$ in such a way that ar $({\text{AOD}}) = {\text{ar}}$ (BOC). Prove that ${\text{ABCD}}$ is a trapezium.
Ans:
Given: Diagonals ${\text{AC}}$ and ${\text{BD}}$ of a quadrilateral ${\text{ABCD}}$ intersect at ${\text{O}}$ in such a way that ar $({\text{AOD}}) = {\text{ar}}$ (BOC).
To Prove: ${\text{ABCD}}$ is a trapezium
It is given in the question that
Area $(\vartriangle {\text{AOD}}) = $ Area $(\vartriangle {\text{BOC}})$
Area $(\vartriangle {\text{AOD}}) + $ Area $(\vartriangle {\text{AOB}}) = $ Area $(\vartriangle {\text{BOC}}) + $ Area $(\vartriangle {\text{AOB}})$
Area $(\vartriangle {\text{ADB}}) = $ Area $(\vartriangle {\text{ACB}})$
We know that triangles on the same base having areas equal to each other lie between the same
parallels.
Therefore, these triangles, $\vartriangle {\text{ADB}}$ and $\vartriangle {\text{ACB}}$, are lying between the same parallels. i.e.,
Therefore, ${\text{ABCD}}$ is a trapezium
16. In the given figure, ar $({\text{DRC}}) = $ ar $({\text{DPC}})$ and ar $({\text{BDP}}) = \operatorname{ar} ({\text{ARC}})$. Show that both the quadrilaterals ${\text{ABCD}}$ and DCPR are trapeziums.
Solution:
Given: ar $({\text{DRC}}) = $ ar $({\text{DPC}})$ and ar $({\text{BDP}}) = \operatorname{ar} ({\text{ARC}})$.
To prove: Both the quadrilaterals ${\text{ABCD}}$ and DCPR are trapeziums.
As $\vartriangle {\text{DRC}}$ and $\vartriangle {\text{DPC}}$ lie on the same base ${\text{DC}}$ and have equal areas, therefore, they must lie between the same parallel lines.
Therefore, DCPR is a trapezium It is also given that
Area $(\vartriangle {\text{BDP}}) = $ Area $(\vartriangle {\text{ARC}})$
Area $(\vartriangle {\text{BDP}}) - $ Area $(\vartriangle {\text{DPC}}) = $ Area $(\vartriangle {\text{ARC}}) - $ Area $(\vartriangle {\text{DRC}})$
$\therefore $ Area $(\Delta {\text{BDC}}) = $ Area $(\vartriangle {\text{ADC}})$
Since $\vartriangle {\text{BDC}}$ and $\vartriangle {\text{ADC}}$ are on the same base ${\text{CD}}$ and have equal areas, they must lie between the same parallel lines.
$\therefore AB{\text{ }}||{\text{ }}CD$
So, ABCD is a trapezium.
Exercise 9.4
1. Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
Ans:
Given: Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas.
To prove: The perimeter of the parallelogram is greater than that of the rectangle.
As the parallelogram and the rectangle have the same base and equal area, So, these will also lie between the same parallels.
Consider the parallelogram ABCD and rectangle ABEF as follows.
Here, it can be observed parallelogram ABCD and rectangle ABEF are between same parallels AB and CF.
We know that opposite sides of a parallelogram or a rectangle are of equal lengths.
So,
AB = EF (For rectangle)
AB = CD (For parallelogram)
$\begin{array}{*{20}{l}} {\therefore CD{\text{ }} = {\text{ }}EF} \\ {\therefore AB{\text{ }} + {\text{ }}CD{\text{ }} = {\text{ }}AB{\text{ }} + {\text{ }}EF{\text{ }}...{\text{ }}\left( 1 \right)} \end{array}$
Of all the line segments that can be drawn to a given line from a point not lying on it, the perpendicular line segment is the shortest.
$\therefore AF{\text{ }} < {\text{ }}AD$
And We know that, $BE{\text{ }} < {\text{ }}BC$
$\therefore AF{\text{ }} + {\text{ }}BE{\text{ }} < {\text{ }}AD{\text{ }} + {\text{ }}BC{\text{ }}...{\text{ }}\left( 2 \right)$
Upon (1) and (2, we obtain
$AB{\text{ }} + {\text{ }}EF{\text{ }} + {\text{ }}AF{\text{ }} + {\text{ }}BE{\text{ }} < {\text{ }}AD{\text{ }} + {\text{ }}BC{\text{ }} + {\text{ }}AB{\text{ }} + {\text{ }}CD$
Perimeter of rectangle ABEF < Perimeter of parallelogram ABCD.
2. In the following figure, D and E are two points on BC such that BD = DE = EC. Show that ar (ABD) = ar (ADE) = ar (AEC). Can you now answer the question that you have left in the ’Introduction’ of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?
(Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide ∆ABC into n triangles of equal areas.)
Ans:
Given: D and E are two locations on BC in the diagram below, and BD = DE = EC. Demonstrate that ar (ABD) = ar (ADE) = ar (AEC).
To find: Can you now respond to the question you posed in the 'Introduction' to this chapter, namely, whether the Budhia field has been divided into three equal parts?
Let us draw a line segment $AL \bot BC.$
We know that, Area of a triangle $ = \dfrac{1}{2} \times $ Base $ \times $ Altitude Area $(\vartriangle {\text{ADE}}) = \dfrac{1}{2} \times {\text{DE}} \times {\text{AL}}$
Area $(\vartriangle {\text{ABD}}) = \dfrac{1}{2} \times {\text{BD}} \times {\text{AL}}$
Area $(\Delta {\text{AEC}}) = \dfrac{1}{2} \times {\text{EC}} \times {\text{AL}}$
It is given in the question that ${\text{DE}} = {\text{BD}} = {\text{EC}}$
$\dfrac{1}{2} \times {\text{DE}} \times {\text{AL}} = \dfrac{1}{2} \times {\text{BD}} \times {\text{AL}} = \dfrac{1}{2} \times {\text{EC}} \times {\text{AL}}$
Area $(\vartriangle {\text{ADE}}) = $ Area $(\vartriangle {\text{ABD}}) = $ Area $(\vartriangle {\text{AEC}})$
It can be observed that Budhia has divided her field into 3 equal parts.
3. In the following figure, ABCD, DCFE and ABFE are parallelograms. Show that $ar{\text{ }}\left( {\Delta ADE} \right){\text{ }} = {\text{ }}ar{\text{ }}\left( {\Delta BCF} \right).$
Ans:
Given: In the following figure, ABCD, DCFE and ABFE are parallelograms.
To prove: $ar{\text{ }}\left( {\Delta ADE} \right){\text{ }} = {\text{ }}ar{\text{ }}\left( {\Delta BCF} \right).$
It is given in the question that ABCD is a parallelogram. We know that opposite sides of a parallelogram are equal.
$\therefore AD{\text{ }} = {\text{ }}BC{\text{ }}...{\text{ }}\left( 1 \right)$
We know that, for parallelograms DCEF and ABFE, it can be proved that
DE = CF ... (2)
And, EA = FB ... (3)
In $\Delta ADE{\text{ , }}\Delta BCF$,
AD = BC [Using equation (1)]
DE = CF [Using equation (2)]
EA = FB [Using equation (3)]
$\therefore \Delta ADE \cong \Delta BCF$ (SSS congruence rule)
$\therefore Area\left( {\Delta ADE} \right){\text{ }} = {\text{ }}Area{\text{ }}\left( {\Delta BCF} \right)$
4. In the following figure, ABCD is parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that $ar{\text{ }}\left( {\Delta BPC} \right){\text{ }} = {\text{ }}ar{\text{ }}\left( {\Delta DPQ} \right)$. [Hint: Join AC.]
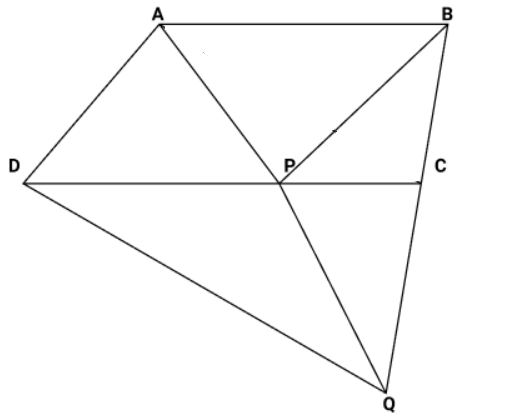
Ans:
Given: In the following figure, ABCD is parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P.
To prove: $ar{\text{ }}\left( {\Delta BPC} \right){\text{ }} = {\text{ }}ar{\text{ }}\left( {\Delta DPQ} \right)$.
It is given in the question that ABCD is a parallelogram.
$AD{\text{ }}\left| {\left| {{\text{ }}BC{\text{ , }}AB{\text{ }}} \right|} \right|{\text{ }}DC$ (Opposite sides of a parallelogram are parallel to each other)
Join point A to point C.
Consider $\vartriangle {\text{APC}}$ and $\Delta {\text{BPC}}$
$\vartriangle {\text{APC}}$ and $\vartriangle {\text{BPC}}$ are lying on the same base ${\text{PC}}$ and between the same parallels ${\text{PC}}$ and ${\text{AB}}$. Therefore,
Area $(\vartriangle {\text{APC}}) = $ Area $(\vartriangle {\text{BPC}}) \ldots $ (1)
In quadrilateral ACDQ, it is given that ${\text{AD}} = {\text{CQ}}$
Since ${\text{ABCD}}$ is a parallelogram,
(Opposite sides of a parallelogram are parallel) ${\text{CQ}}$ is a line segment which is obtained when line segment ${\text{BC}}$ is produced.
We have, ${\text{AC}} = {\text{DQ}}$ and
Hence, ACQD is a parallelogram.
Consider BDCQ and BACQ These are on the same base ${\text{CQ}}$ and between the same parallels ${\text{CQ}}$ and ${\text{AD}}$.
Therefore, Area $(\Delta {\text{DCQ}}) = $ Area $(\vartriangle {\text{ACQ}})$
$\therefore $ Area $(\Delta {\text{DCQ}}) - $ Area $(\Delta {\text{PQC}}) = $ Area $(\Delta {\text{ACQ}}) - $ Area $(\Delta {\text{PQC}})$
$\therefore $ Area $(\Delta {\text{DPQ}}) = $ Area $(\vartriangle {\text{APC}}) \ldots (2)$
From equations (1) and (2), we obtain
Area $(\Delta {\text{BPC}}) = $ Area $(\Delta {\text{DPQ}})$
5. In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
(i) $\operatorname{ar} ({\text{BDE}}) = \dfrac{1}{4}\operatorname{ar} ({\text{ABC}})$
(ii) ar $({\text{BDE}}) = \dfrac{1}{2}$ ar (BAE)
(iii) ar $({\text{ABC}}) = 2$ ar $({\text{BEC}})$
(iv) ar (BFE) = ar (AFD)
(v) ar $({\text{BFE}}) = 2$ ar (FED)
(vi) ar $({\text{FED}}) = \dfrac{1}{8}$ ar (AFC)
(Hint: Join EC and AD. Show that $BE{\text{ }}\left| {\left| {{\text{ }}AC{\text{ , }}DE{\text{ }}} \right|} \right|{\text{ }}AB$etc.)
Ans:
Given: In the following figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F.
To prove: (i) $\operatorname{ar} ({\text{BDE}}) = \dfrac{1}{4}\operatorname{ar} ({\text{ABC}})$
(ii) ar $({\text{BDE}}) = \dfrac{1}{2}$ ar (BAE)
(iii) ar $({\text{ABC}}) = 2$ ar $({\text{BEC}})$
(iv) ar (BFE) = ar (AFD)
(v) ar $({\text{BFE}}) = 2$ ar (FED)
(vi) ar $({\text{FED}}) = \dfrac{1}{8}$ ar (AFC)
(i) Let G and H be the mid-points of side AB and AC. Line segment GH is joining the mid-points and is parallel to third side. So, BC will be half of length of BC (mid-point theorem).
$\therefore {\text{GH}} = \dfrac{1}{2}{\text{BC}}$ and
$\therefore {\text{GH}} = {\text{BD}} = {\text{DC}}$ and (D is the mid-point of ${\text{BC}}$ )
Similarly,
- $\quad {\text{GD}} = {\text{HC}} = {\text{HA}}$
- ${\text{HD}} = {\text{AG}} = {\text{BG}}$
Therefore, clearly $\vartriangle {\text{ABC}}$ is divided into 4 equal equilateral triangles viz $\vartriangle {\text{BGD}},\Delta {\text{AGH}},\vartriangle {\text{DHC}}$ and $\Delta {\text{GHD}}$
In other words, $\Delta {\text{BGD}} = \dfrac{1}{4}\Delta {\text{ABC}}$
Now consider $\vartriangle {\text{BDG}}$ and $\Delta {\text{BDE}}$
${\text{BD}} = {\text{BD}}$ (Common base) As both triangles are equilateral triangle, we can say ${\text{BG}} = {\text{BE}}$
${\text{DG}} = {\text{DE}}$
Therefore, $\Delta {\text{BDG}} \cong \Delta {\text{BDE}}[{\text{By}}$ SSS congruency]
Thus, area $(\vartriangle {\text{BDG}}) = $ area $(\vartriangle {\text{BDE}})$
$\operatorname{ar} (\Delta {\text{BDE}}) = \dfrac{1}{4}$ ar $(\Delta {\text{ABC}})$
Hence proved
(ii) Area ( $(\vartriangle {\text{BDE}}) = $ Area ( $\vartriangle {\text{AED}})$ (Common base DE and ) Area $(\vartriangle {\text{BDE}}) - $ Area $(\vartriangle {\text{FED}}) = $ Area $(\vartriangle {\text{AED}}) - $ Area $(\vartriangle {\text{FED}})$
Area $(\vartriangle {\text{BEF}}) = $ Area $(\vartriangle {\text{AFD}})$
Now, Area $(\vartriangle {\text{ABD}}) = $ Area $(\vartriangle {\text{ABF}}) + $ Area $(\vartriangle {\text{AFD}})$
Area $(\vartriangle {\text{ABD}}) = $ Area $(\vartriangle {\text{ABF}}) + $ Area $(\vartriangle {\text{BEF}})$ [From equation (1)] Area $(\vartriangle {\text{ABD}}) = $ Area $(\vartriangle {\text{ABE}})$
AD is the median in $\vartriangle {\text{ABC}}$.
$\operatorname{ar} (\vartriangle {\text{ABD}}) = \dfrac{1}{2}\operatorname{ar} (\vartriangle {\text{ABC}})$
$ = \dfrac{4}{2}\operatorname{ar} (\Delta {\text{BDE}})$
(As proved earlier)
ar $(\vartriangle {\text{ABD}}) = 2\operatorname{ar} (\Delta {\text{BDE}})$ (3)
From (2) and (3), we obtain $2\operatorname{ar} (\vartriangle {\text{BDE}}) = \operatorname{ar} (\vartriangle {\text{ABE}})$
ar $({\text{BDE}}) = \dfrac{1}{2}$ ar $({\text{BAE}})$
(iii)
$\operatorname{ar} (\vartriangle {\text{ABE}}) = \operatorname{ar} (\vartriangle {\text{BEC}})$ (Common base BE and BEI|AC)
ar $(\vartriangle ABF) + \operatorname{ar} (\Delta BEF) = \operatorname{ar} (\Delta BEC)$
Using equation (1), we obtain
$\operatorname{ar} (\vartriangle ABF) + \operatorname{ar} (\vartriangle AFD) = \operatorname{ar} (\Delta BEC)$
$\operatorname{ar} (\vartriangle ABD) = \operatorname{ar} (\Delta BEC)$
$\dfrac{1}{2}\operatorname{ar} (\vartriangle {\text{ABC}}) = \operatorname{ar} ({\text{ABEC}})$
$\operatorname{ar} (\vartriangle ABC) = 2\operatorname{ar} (\Delta BEC)$
(iv) It is seen that $\Delta {\text{BDE}}$ and ar $\vartriangle {\text{AED}}$ he on the same base $({\text{DE}})$ and between the parallels ${\text{DE}}$ and ${\text{AB}}$.
$\therefore $ ar $(\Delta {\text{BDE}}) = \operatorname{ar} (\Delta {\text{AED}})$
$\therefore $ ar $(\Delta {\text{BDE}}) - \operatorname{ar} (\Delta {\text{FED}}) = \operatorname{ar} (\Delta {\text{AED}}) - \operatorname{ar} (\Delta {\text{FED}})$
$\therefore $ ar $(\Delta {\text{BFE}}) = \operatorname{ar} (\Delta {\text{AFD}})$
(v) Let ${\text{h}}$ be the height of vertex ${\text{E}}$, corresponding to the side ${\text{BD}}$ in $\vartriangle {\text{BDE}}$. Let ${\text{H}}$ be the height of vertex ${\text{A}}$, corresponding to the side ${\text{BC}}$ in $\vartriangle {\text{ABC}}$. In (i), it was shown that ar $({\text{BDE}}) = \dfrac{1}{4}$ ar $({\text{ABC}})$
In (iv), it was shown that ar $(\Delta {\text{BFE}}) = \operatorname{ar} (\vartriangle {\text{AFD}})$.
$\therefore $ ar $(\Delta {\text{BFE}}) = \operatorname{ar} (\Delta {\text{AFD}})$
$ = 2$ ar $(\Delta {\text{FED}})$
Hence,
(vi)
$\operatorname{ar} \left( {{\Delta _{{\text{AFC}})}} = \operatorname{ar} \left( {{\Delta _{{\text{AFD}})}} + \operatorname{ar} \left( {{\Delta _{{\text{ADC}}}}} \right) = 2\operatorname{ar} \left( {{\Delta _{{\text{FED}}}}} \right) + \dfrac{1}{2}\operatorname{ar} \left( {{\Delta _{{\text{ABC}}}}} \right)[{\text{using}}({\text{v}})} \right.} \right.$
$ = 2$ ar $(\Delta {\text{FED}}) + \dfrac{1}{2}[4 \times \operatorname{ar} (\Delta {\text{BDE}})][$ Using result of part (i)]
$ = 2$ ar $(\Delta {\text{FED}}) + 2\operatorname{ar} (\Delta {\text{BDE}}) = 2\operatorname{ar} (\Delta {\text{FED}}) + 2$ ar $(\Delta {\text{AED}})$
[ $\Delta {\text{BDE}}$ and $\Delta {\text{AED}}$ are on the same base and between same parallels] $ = 2$ ar $(\Delta {\text{FED}}) + 2[\operatorname{ar} (\Delta {\text{AFD}}) + \operatorname{ar} (\Delta {\text{FED}})]$
$ = 2\operatorname{ar} (\Delta {\text{FED}}) + 2$ ar $\left( {{\Delta _{{\text{AFD}}}}} \right) + 2$ ar ( $\left. {\Delta {\text{FED}}} \right)$ (Using (viii))
$ = 4$ ar $(\Delta {\text{FED}}) + 4$ ar $(\Delta {\text{FED)}}$
$ \Rightarrow \operatorname{ar} (\Delta {\text{AFC}}) = 8\operatorname{ar} (\Delta {\text{FED}})$
$ \Rightarrow \operatorname{ar} (\Delta {\text{FED}}) = \dfrac{1}{8}\operatorname{ar} (\Delta {\text{AFC}})$
6. Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that [Hint: From A and C, draw perpendiculars to BD]
Ans:
Given: A quadrilateral ABCD, in which diagonals AC and BD intersect each other at point E.
To prove: $ar\left( {{\text{ }}AED} \right){\text{ }}ar\left( {{\text{BEC}}} \right) = ar\left( {{\text{ }}ABE} \right){\text{ }}ar\left( {{\text{CDE }}} \right)$
Construction: From ${\text{A}}$, draw $AM \bot BD{\text{AM}}$ BD and from ${\text{C}}$, draw $CN \bot BD$.
Proof $:\operatorname{ar} (\Delta {\text{ABE}}) = \dfrac{1}{2} \times {\text{BE}} \times {\text{AM}}$
$\operatorname{ar} (\vartriangle {\text{AED}}) = \dfrac{1}{2} \times {\text{DE}} \times {\text{AM}} \ldots \ldots \ldots $
Dividing eq.(ii) by (i), we get, $\dfrac{{\operatorname{ar} (\Delta {\text{AED}})}}{{{\text{ar}}(\vartriangle {\text{ABE}})}} = \dfrac{{\dfrac{1}{2} \times {\text{DE}} \times {\text{AM}}}}{{\dfrac{1}{2} \times {\text{BE}} \times {\text{AM}}}}$
$ \Rightarrow \dfrac{{\operatorname{ar} (\vartriangle {\text{AED}})}}{{{\text{ar}}(\vartriangle {\text{ABE}})}} = \dfrac{{{\text{DE}}}}{{{\text{BE}}}} \ldots \ldots \ldots \ldots \ldots ..$ (iii)
Similarly $\dfrac{{\operatorname{ar} (\Delta {\text{CDE}})}}{{\operatorname{ar} (\vartriangle {\text{BEC}})}} = \dfrac{{{\text{DE}}}}{{{\text{BE}}}}$.......(iv)
From eq.(iii) and (iv), we get $\dfrac{{\operatorname{ar} (\vartriangle {\text{AED}})}}{{{\text{ar}}(\vartriangle {\text{ABE}})}} = \dfrac{{\operatorname{ar} (\Delta {\text{CDE}})}}{{\operatorname{ar} (\Delta {\text{BEC}})}}$
$ \Rightarrow \operatorname{ar} (\vartriangle {\text{AED}}) \times \operatorname{ar} (\Delta {\text{BEC}}) = \operatorname{ar} (\Delta {\text{ABE}}) \times \operatorname{ar} (\Delta {\text{CDE}})$
Hence prored.
7. ${\text{P}}$ and ${\text{Q}}$ are respectively the mid-points of sides ${\text{AB}}$ and ${\text{BC}}$ of a triangle ${\text{ABC}}$ and ${\text{R}}$ is the mid-point of ${\text{AP}}$, show that
(i) ar $({\mathbf{PRQ}}) = \dfrac{1}{2}\operatorname{ar} ({\text{ARC}})$
(ii) $\operatorname{ar} ({\text{RQC}}) = \dfrac{3}{8}\operatorname{ar} ({\text{ABC}})$
(iii) ar $({\text{PBQ}}) = \operatorname{ar} ({\text{ARC}})$
Solution:
Given: ${\text{P}}$ and ${\text{Q}}$ are respectively the mid-points of sides ${\text{AB}}$ and ${\text{BC}}$ of a triangle ${\text{ABC}}$ and ${\text{R}}$ is the mid-point of ${\text{AP}}$,
To prove:
(i) ar $({\mathbf{PRQ}}) = \dfrac{1}{2}\operatorname{ar} ({\text{ARC}})$
(ii) $\operatorname{ar} ({\text{RQC}}) = \dfrac{3}{8}\operatorname{ar} ({\text{ABC}})$
(iii) ar $({\text{PBQ}}) = \operatorname{ar} ({\text{ARC}})$
(i) ${\text{PC}}$ is the median of $\vartriangle {\text{ABC}}$.
$\therefore \operatorname{ar} (\Delta {\text{BPC}}) = \operatorname{ar} (\Delta {\text{APC}}) \ldots \ldots \ldots $ (i)
${\text{RC}}$ is the median $\Delta $ of ${\text{APC}}$.
- ar $(\Delta {\text{ARC}}) = \dfrac{1}{2}$ ar $(\Delta {\text{APC}}) \ldots \ldots \ldots $ (ii)
(Median dirides the triangle into two triangles of equal area)
${\text{PQ}}$ is the median of $\vartriangle {\text{BPC}}$
$\operatorname{ar} (\Delta {\text{PQC}}) = \dfrac{1}{2}{\text{ar}}(\Delta {\text{BPC}}) \ldots \ldots ..$ (iii)
From eq. (i) and (iii), we get, $\operatorname{ar} (\Delta {\text{PQC}}) = \dfrac{1}{2}$ ar $(\Delta {\text{APC}}) \ldots \ldots ..$ (iv)
From eq. (ii) and (iv), we get, ar $(\Delta {\text{PQC}}) = {\text{ar}}(\Delta {\text{ARC}}) \ldots \ldots ...({\text{v}})$
We are given that ${\text{P}}$ and ${\text{Q}}$ are the mid-points of ${\text{AB}}$ and ${\text{BC}}$ respectively. and ${\text{PA}} = \dfrac{1}{2}{\text{AC}}$
$ \Rightarrow $ ar $(\Delta {\text{APQ}}) = {\text{ar}}(\Delta {\text{PQC}}) \ldots \ldots \ldots $ (vi) [triangles between same parallel are equal in area] From eq. ( $v$ ) and (vi), we get ar $(\Delta {\text{APQ}}) = a(\Delta {\text{ARC}}) \ldots \ldots ..$ (vii)
$\mathbb{R}$ is the mid-point of ${\text{AP}}$. Therefore ${\text{RQ}}$ is the median of $\vartriangle {\text{APQ}}$. $ - \operatorname{ar} (\Delta {\text{PRQ}}) = \dfrac{1}{2}{\text{ar}}(\Delta {\text{APQ}}) \ldots \ldots ..$ (viii)
From (ii) and (iii), we get, ar $(\Delta {\text{PRQ}}) = \dfrac{1}{2}{\text{ar}}(\Delta {\text{ARC}})$
(ii) ${\text{PQ}}$ is the median of $\Delta {\text{BPC}}$ ar $(\Delta {\text{PQC}}) = \dfrac{1}{2}$ ar $(\Delta {\text{BPC}}) = \dfrac{1}{2} \times \dfrac{1}{2}a(\Delta {\text{ABC}}) = \dfrac{1}{4}$ ar $\left( {{\Delta _{{\text{ABC}}}}} \right) \ldots \ldots \ldots $.(ix)
Also ar $(\Delta {\text{PRC}}) = \dfrac{1}{2}$ ar $(\Delta {\text{APC}})[{\text{Using}}({\text{r}} \cdot )]$
$ \Rightarrow \operatorname{ar} (\Delta {\text{PRC}}) = \dfrac{1}{2} \times \dfrac{1}{2}$ ar $\left( {{\Delta _{{\text{ABC}}}}} \right) = \dfrac{1}{4}\operatorname{ar} \left( {{\Delta _{{\text{ABC}}}}} \right) \ldots \ldots \ldots .({\text{x}})$
Adding eq. (ix) and ( ${\text{x}}$ ), we get, ar $(\Delta {\text{PQC}}) + \operatorname{ar} (\Delta {\text{PRC}}) = \left( {\dfrac{1}{4} + \dfrac{1}{4}} \right){\text{ar}}(\Delta {\text{ABC}})$
$ \Rightarrow $ar (quad. $\left. {{\text{PQCR}}} \right) = \dfrac{1}{2}$ ar $(\Delta {\text{ABC}}) \ldots \ldots \ldots ..({\text{xi}})$
Subtracting ar ( $\vartriangle $ PRQ) from the both sides, ar (quad. ${\text{PQCR}}) - \operatorname{ar} (\Delta {\text{PRQ}}) = \dfrac{1}{2}$ ar $(\Delta {\text{ABC}}) - \operatorname{ar} (\Delta {\text{PRQ}})$
$ \Rightarrow \operatorname{ar} (\Delta {\text{RQC}}) = \dfrac{1}{2}$ ar $(\Delta {\text{ABC}}) - \dfrac{1}{2}$ ar $(\Delta {\text{ARC}})[$ Using result (i)]
${ \Rightarrow _{ar}}\left( {{\Delta _{ARC}}} \right) = \dfrac{1}{2}$ ar $(\Delta ABC) - \dfrac{1}{2} \times \dfrac{1}{2}$ ar $(\Delta APC)$
${ \Rightarrow _{{\text{ar }}}}\left( {{\Delta _{{\text{RQC}}}}} \right) = \dfrac{1}{2}$ ar $\left( {{\Delta _{{\text{ABC}}}}} \right) - \dfrac{1}{4}$ ar ${\Delta _{APC}}$
${ \Rightarrow _{ar}}\left( {{\Delta _{RQC}}} \right) = \dfrac{1}{2}$ ar $\left( {{\Delta _{ABC}}} \right) - \dfrac{1}{4} \times \dfrac{1}{2}$ ar $\left( {{\Delta _{ABC}}} \right)\left[ {PC} \right.$ is median of $\Delta ABC]$
${ \Rightarrow _{ar}}\left( {{\Delta _{RQC}}} \right) = \dfrac{1}{2}ar(\Delta ABC) - \dfrac{1}{8}ar(\Delta ABC)$
${ \Rightarrow _{\operatorname{ar} }}(\Delta {\text{RQC}}) = \left( {\dfrac{1}{2} - \dfrac{1}{8}} \right) \times \operatorname{ar} (\Delta {\text{ABC}})$
${ \Rightarrow _{\operatorname{ar} }}\left( {{\Delta _{{\text{RQC}}}}} \right) = \dfrac{3}{8}$ ar $\left( {{\Delta _{{\text{ABC}}}}} \right)$
(iii) ar ( $\Delta {\text{PRQ}}) = \dfrac{1}{2}$ ar ( $\left. {\vartriangle {\text{ARC}}} \right)[$ Using result (i)] $ \Rightarrow 2{\text{ar}}(\Delta {\text{PRQ}}) = \operatorname{ax} (\vartriangle {\text{ARC}})$..(xii)
ar $(\Delta {\text{PRQ}}) = \dfrac{1}{2}$ ar $(\vartriangle {\text{APQ}})\left[ {{\text{RQ}}} \right.$ is the median of ${\Delta _{{\text{APQ}}]}} \ldots \ldots \ldots ..$ (xiii)
But ar $(\Delta {\text{APQ}}) = $ ar $(\Delta {\text{PQC}})[$ Using reason of eq. (vi)] $ \ldots \ldots \ldots $ (xiv) From eq. (xiii) and (xiv), we get, ar $(\Delta {\text{PRQ}}) = \dfrac{1}{2}$ ar $(\Delta {\text{PQC}}) \ldots \ldots \ldots ..({\text{xv}})$
From eq. (x) and ( $x$ i), we get,
ar $(\Delta {\text{PRQ}}) = \dfrac{1}{2}$ ar $(\Delta {\text{BPQ}}) \ldots \ldots $... $({\text{xvii}})$
Now from (xii) and (xvii), we get, $2 \times \dfrac{1}{2}ar(\vartriangle BPQ) = ar\left( {{\Delta _{{\text{ARC}}}}} \right) \Rightarrow \operatorname{ar} (\Delta {\text{BPQ}}) = \operatorname{ar} (\Delta {\text{ARC}})$
8. In the following figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment $AX \bot DE$ meets BC at Y.
(i) $\Delta {\text{MBC}} \cong \vartriangle {\text{ABD}}$
(ii) $\operatorname{ar} ({\text{BYXD}}) = 2\operatorname{ar} ({\text{MBC}})$
(iii) $\operatorname{ar} ({\text{BYXD}}) = 2\operatorname{ar} ({\text{ABMN}})$
(iv) $\Delta {\text{FCB}} \cong \Delta {\text{ACE}}$
(v) $\operatorname{ar} ({\text{CYXE}}) = 2\operatorname{ar} ({\text{FCB}})$
(vi) $\operatorname{ar} ({\text{CYXE}}) = \operatorname{ar} ({\text{ACFG}})$
(vii) $\operatorname{ar} ({\text{BCED}}) = \operatorname{ar} ({\text{ABMN}}) + \operatorname{ar} ({\text{ACFG}})$
Note: Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in class ${\text{X}}$.
Solution:
Given: In the following figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment $AX \bot DE$ meets BC at Y.
To prove: (i) $\Delta {\text{MBC}} \cong \vartriangle {\text{ABD}}$
(ii) $\operatorname{ar} ({\text{BYXD}}) = 2\operatorname{ar} ({\text{MBC}})$
(iii) $\operatorname{ar} ({\text{BYXD}}) = 2\operatorname{ar} ({\text{ABMN}})$
(iv) $\Delta {\text{FCB}} \cong \Delta {\text{ACE}}$
(v) $\operatorname{ar} ({\text{CYXE}}) = 2\operatorname{ar} ({\text{FCB}})$
(vi) $\operatorname{ar} ({\text{CYXE}}) = \operatorname{ar} ({\text{ACFG}})$
(vii) $\operatorname{ar} ({\text{BCED}}) = \operatorname{ar} ({\text{ABMN}}) + \operatorname{ar} ({\text{ACFG}})$
(i) We know that each angle of a square is ${90^\circ }$. Hence, $\angle {\text{ABM}} = \angle {\text{DBC}} = {90^\circ }$
$\therefore \angle {\text{ABM}} + \angle {\text{ABC}} = \angle {\text{DBC}} + \angle {\text{ABC}}$
$\therefore \angle {\text{MBC}} = \angle {\text{ABD}}$
In $\vartriangle {\text{MBC}}$ and $\vartriangle {\text{ABD}}$,
$\angle {\text{MBC}} = \angle {\text{ABD}}$ (Proved abore)
${\text{MB}} = {\text{AB}}$ (Sides of square ABMIN) ${\text{BC}} = {\text{BD}}$ (Sides of square BCED)
$\therefore \vartriangle {\text{MBC}} \cong \vartriangle {\text{ABD}}$ (SAS congruence rule)
(ii) We have $\Delta {\text{MBC}} \cong \Delta {\text{ABD}}$
$\therefore $ ar $(\Delta {\text{MBC}}) = \operatorname{ar} (\vartriangle {\text{ABD}}) \ldots $ (1)
It is given that ${\text{AX}} \bot {\text{DE}}$ and ${\text{BD}} \bot {\text{DE}}$ (Adjacent sides of square BDEC)
(Two lines perpendicular to same line are parallel to each other) $\vartriangle {\text{ABD}}$ and parallelogram BYXD are on the same base BD and between the same parallels BD and ${\text{AX}}$. Area $(\Delta {\text{YXD}}) = 2$ Area $(\Delta {\text{MBC}})$ [Using equation (1)] \ldots.. (2)
(iii) $\vartriangle {\text{MBC}}$ and parallelogram ${\text{ABMN}}$ are lying on the same base ${\text{MB}}$ and between same parallels ${\text{MB}}$ and ${\text{NC}}$. 2 ar $(\Delta {\text{MBC}}) = \operatorname{ar} ({\text{ABMN}})$
ar $(\Delta {\text{YXD}}) = \operatorname{ar} ({\text{ABMN}})$ [Using equation (2)] ... (3)
(iv) We know that each angle of a square is ${90^\circ }$. $\therefore \angle {\text{FCA}} = \angle {\text{BCE}} = {90^\circ }$
$\therefore \angle {\text{FCA}} + \angle {\text{ACB}} = \angle {\text{BCE}} + \angle {\text{ACB}}$
$\therefore \angle {\text{FCB}} = \angle {\text{ACE}}$
In $\vartriangle {\text{FCB}}$ and $\Delta {\text{ACE}}$,
$\angle {\text{FCB}} = \angle {\text{ACE}}$
${\text{FC}} = {\text{AC}}$ (Sides of square ACFG) ${\text{CB}} = {\text{CE}}$ (Sides of square BCED) $\Delta {\text{FCB}} \cong \Delta {\text{ACE}}$ (SAS congruence rule)
(v) It is given that ${\text{AX}} \bot {\text{DE}}$ and ${\text{CE}} \bot {\text{DE}}$ (Adjacent sides of square ${\text{BDEC}}$ ) Hence, (Two lines perpendicular to the same line are parallel to each other) Consider BACE and parallelogram CYXE BACE and parallelogram CYXE are on the same base CE and between the same parallels CE and AX.
$\therefore \operatorname{ar} (\Delta {\text{YXE}}) = 2$ ar ( $\Delta {\text{ACE}}) \ldots $... (4)
We had proved that
$\therefore \Delta {\text{FCB}} \cong \vartriangle {\text{ACE}}$
$\operatorname{ar} (\Delta {\text{FCB}}) \cong \operatorname{ar} (\Delta {\text{ACE}}) \ldots (5)$
On comparing equations (4) and (5), we obtain
$\operatorname{ar} ({\text{CYXE}}) = 2$ ar $(\Delta {\text{FCB}}) \ldots (6)$
(vi) Consider BFCB and parallelogram ACFG BFCB and parallelogram ACFG are lying on the same base CF and between the same parallels ${\text{CF}}$ and ${\text{BG}}$.
$\therefore $ ar $({\text{ACFG}}) = 2$ ar $(\Delta {\text{FCB}})$
$\therefore $ ar $({\text{ACFG}}) = \operatorname{ar} ({\text{CYXE}})[$ Using equation $(6)] \ldots (7)$
(vii) From the figure, it is evident that ar $(\Delta {\text{CED}}) = \operatorname{ar} (\Delta {\text{YXD}}) + \operatorname{ar} ({\text{CYXE}})$
$\therefore $ ar $(\Delta {\text{CED}}) = \operatorname{ar} ({\text{ABMN}}) + \operatorname{ar} ({\text{ACFG}})$ (Using equations (3) and (7)).
NCERT Solutions for Class 9 Maths Chapter 9 Areas of Parallelogram and Triangle - PDF Download
NCERT Solutions for Class 9 Maths - Free PDF Download
For those students having trouble finding reliable Class 9 Chapter 9 guides, you now have nothing to worry about as we’ve got you covered. The comprehensive solutions offered in the NCERT Class 9 Maths Chapter 9 PDF will help prepare you well for your exam. Gain insights into how exactly you can learn about different concepts offered in this chapter with ease. Go to the official website of Vedantu to download the PDF of NCERT Maths Class 9 Chapter 9.
You can opt for Chapter 9 - Areas of Parallelograms and Triangles NCERT Solutions for Class 9 Maths PDF for Upcoming Exams and also You can Find the Solutions of All the Maths Chapters below.
NCERT Solutions for Class 9 Maths
Chapter 9 - Areas of Parallelograms and Triangles
NCERT Solutions for Class 9 Maths Chapter 9
9.1 Introduction
Areas of Parallelograms and Triangles is a brief chapter in Unit IV, Geometry. This chapter is elaborated to help students understand every concept that falls under areas of parallelograms and triangles. This chapter is divided into several subcategories to explain precise details to students. The introduction section of the chapter aims at giving a brief overview of the topic.
Here, students will learn the definition of area and how it is a number or figure linked with a specific part of the plane surrounded by that respective figure. Further, you will also learn about different figures in that very base and amid those parallels. You will learn about this more accurately with the help of distinguished figures and explanations.
In a nutshell, all the solutions offered in this chapter will give students an edge in their exams. They will also learn about parallelograms between the same parallels and the same base. Different theorems, numerical, and explanations will help you grasp this. Overall, the Area of Parallelogram and Triangle Class 9 PDF aims at assisting students in learning and falling in love with the concept. PDFs can be referred to offline and also help students enjoy the process of learning.
9.2 Figures on the Same Base and Between the Same Parallels
In this section, students will learn thoroughly about different figures between the same parallels and base. Two figures are primarily said to be between the same parallels and the same base if they comprise a common base or side and the vertex opposite to this common base of every figure are on a line parallel to this base. Students will learn more about this by examining different figures.
The section consists of several examples to help students understand this concept clearly. This section is comparatively easy to understand as it gives students clarity on what they’ll be dealing with throughout the chapter.
9.3 Parallelograms on the Same Base and Between the Same Parallels
The next section is also easy to understand if you pay attention to the essential details. Chapter 9 Class 9 will give students insights into different figures, rather parallelograms on the same base and between the same parallels. You will be asked to take a careful look at distinguishing figures to understand this concept.
Students will learn more about this concept by solving numerical and theorems. This section consists of one theorem that is easy to understand and can be solved with ease. Students should go through all the examples and practise the exercise questions to become familiar with this concept. Students are also advised to practice the theorems regularly.
9.4 Triangles on the Same Base and Between the Same Parallels
This section is of prime importance. It contains different examples that will help students understand more about triangles on the same base and between the same parallels. In this section, students will have to perform different activities to prove the concept. The Class 9th Maths Chapter 9 PDF includes different examples and elaborations of the definitions to help students know more about this topic.
This section also consists of a theorem- Two triangles lying on the same base and between the same parallels are said to be equal in area. The NCERT solutions of maths class 9 chapter 9 PDF will teach you how to solve this theorem and how you can use this theorem to solve numericals further.
9.5 Summary
Once you finish learning about the three focal concepts that this chapter covers, you can go through the summary. The summary helps you sum up what you’ve learned so far in the chapter.
It will help students strengthen their understanding of the core concepts of areas of parallelograms and triangles. It will also help them remember all the elements that are essential for acing exams. All the theorems, definitions, and formulas are summed up in this section.
Exercises
There are four exercises in this chapter. Out of these, exercise 9.4 is optional. You can go through the NCERT Solutions Maths Class 9 Chapter 9 PDF to get solutions to the exercise questions. Every section comprises one exercise to help students grasp the knowledge they’ve gained so far better.
Key Learnings from NCERT Solutions for Class 9 Maths Chapter 9 Areas of Parallelograms and Triangles
Chapter 9 Areas of parallelograms and triangles is a very important chapter for coordinate geometry in Class 9 Maths. NCERT Solutions for Class 9 Maths Chapter 9 are mainly based on topics such as the introduction of areas of parallelograms and triangles, triangles as well as parallelograms on the same base and between the same parallels, and figures on the same base and between the same parallels. Below are some of the key learnings from this chapter. Students are advised to memorise these points that will be highly beneficial to score well in the final exam.
Area of a triangle = ½ x Base x Altitude
Area of a parallelogram = Base x Height
The area of a figure can be defined as a number associated with the part of the plane enclosed by that figure.
Two congruent figures may have equal areas but the converse is not true.
Two figures are said to be on the same base and between the same parallels, if they have a common base (side) and the vertices (or the vertex) opposite to the common base of each figure lie on a line parallel to the base.
Parallelograms on the same base (or equal bases) and between the same parallels are equal in area.
Parallelograms on the same base (or equal bases) and having equal areas lie between the same parallels.
Triangles on the same base (or equal bases) and between the same parallels are equal in area.
Triangles on the same base (or equal bases) and having equal areas lie between the same parallels.
A median of a triangle divides it into two triangles of equal areas.
Understanding the basics of these concepts is very crucial for students as this serves as the base for higher grade Maths studies (especially trigonometry, calculus, and coordinate geometry).
NCERT Solution Class 9 Maths of Chapter 9 Areas of Parallelograms and Triangles All Exercises.
Chapter 9 - Areas of Parallelograms and Triangles Exercises in PDF Format | |
1 Questions & Solutions (1 Short Answer) | |
6 Questions & Solutions (5 Short Answers, 1 Long Answer) | |
16 Questions & Solutions (12 Short Answers, 4 Long Answers) | |
8 Questions & Solutions (4 Short Answers, 1 Long Answer, 3 Very Long Answers) | |
Students are advised to solve all these exercise questions, including the optional exercise questions. They can, in this way, become more familiar with the type of questions that may encounter in their exams.
Key Features of NCERT Solutions for Class 9 Maths Chapter 9
Practising numerical and theorems is an extremely crucial step in preparing for your exams. With the Class 9 Maths Solution Chapter 9 PDF, students can ensure completing every concept of Class 9 Maths Chapter 9. Here are some prime features of Maths NCERT Solutions Class 9 Chapter 9:
All explanations for different concepts are made easier to help students understand more clearly.
The PDF solutions will help students gain deep insights into how they can solve the numerical.
Students can revise from these PDFs to have the best chance at scoring good marks in their upcoming exams.





















FAQs on NCERT Solutions for Class 9 Maths Chapter 9 - Areas Of Parallelograms And Triangles
Q1. What does Maths Class 9 Ch 9 entail?
Ans: Class 9 Chapter 9 Areas Of Parallelograms And Triangles give students a clear idea of how they can calculate the areas of different parallelograms and triangles. The chapter also introduces students to some core concepts of areas and parallelograms. These include- figures on the same base and between the same parallels, triangles on the same base and between the same parallels, and so on. Students can access the NCERT Class 9 Chapter 9 PDF to get a deeper understanding of these topics.
Q2. Why should I choose NCERT Solutions For Class 9 Chapter 9?
Ans: NCERT solutions are designed to help students get over obstacles concerning understanding the chapter. NCERT PDF on Class 9 Chapter 9 aims at preparing students to answer exercise questions with ease. All the elaborate questions given here will prepare students to ace their exams.
Q4. What is the Area Of Triangle in the Class 9 syllabus?
Ans: Chapter 9 in Class 9 Maths NCERT deals in the area of triangles and parallelograms. By definition, a triangle’s area is the complete space occupied by the three sides of an enclosed figure in a 2-dimensional plane. The area of a triangle is calculated by dividing the product of its base and height by 2, i.e., A = 1/2 × b × h. NCERT Solutions for Class 9 Maths Vedantu gives a clear description of the same.
Q4. How do you prove a Parallelogram Class 9?
Ans: There are many properties of a parallelogram that can prove that it is a parallelogram. These properties are:
The opposite sides are parallel.
Opposite angles are equal.
Each diagonal of a parallelogram divides it into two similar triangles.
Bisecting diagonals.
Consecutive angles are supplementary, i.e. sum is 180.
For more questions and solutions on parallelograms, visit the page NCERT Solutions for Class 9 Maths and download the solution PDFs for free.
Q5. Can we consider any side of a parallelogram is a base while calculating its area?
Ans: Yes, we can consider any side of a parallelogram as a base and use it for calculating its area. To this base, a height can be drawn at any angle situated perpendicular to that side. This way the formula of the area of a parallelogram can be applied here to calculate the area. You can refer to Vedantu NCERT Solutions for Class 9 Maths Chapter 9 for further clarification.
Q6. What is Heron's Formula Class 9?
Ans: The area of a triangle can be calculated easily when the length of all its sides is known, using the formula known as Heron’s Formula. For using this formula to calculate the area of the triangle, one does not need to know the angle measurements or other distances in the triangle. You can refer to Vedantu’s NCERT Solutions for Class 9 Maths Chapter 9 for further clarification. You can also download the free PDF of the solution from the Vedantu app.
Q7. What are the uses of NCERT Solutions for Chapter 9 in Class 9 Maths?
Ans: NCERT Solutions for Chapter 9 in Class 9 Maths gives a descriptive explanation about the chapter, its concepts and the pattern of questions. NCERT Solutions also provide the answers for all the questions in the exercise which the students can refer to, understand and learn from. Practising these will help students get good marks in their examination and also gain knowledge regarding the topic. You can refer to Vedantu page NCERT Solutions for Class 9 Maths for further information.



