NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals - FREE PDF Download






NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals

 Share
Share























FAQs on NCERT Solutions for Class 9 Maths Chapter 8 Quadrilaterals
1. What is the relation between square, Rectangle, and Rhombus?
A Square is a Rectangle and a Rhombus. But Rhombus and Rectangle are not Squares.
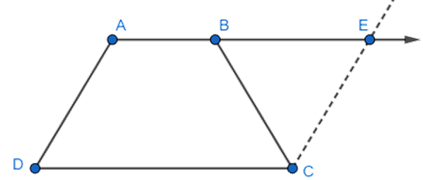
2. What is the relation between a trapezium and a parallelogram?
A parallelogram is a trapezium but a trapezium is not a parallelogram.
3. How to avoid silly mistakes?
Paying attention to the theorems and their usage in the notes provided would minimize the silly mistakes. A clear understanding of the steps involved and practice is the key. Going through the NCERT Solutions for Class 9 Chapter 8 would clear all your dangling doubts and would learn a lot of alternative steps.
4. How to increase our score in CBSE examinations?
CBSE test papers mainly test the understanding of the students. So a clear explanation for every step would help you score more. As the Quadrilateral chapter involves long steps of proof, the reason for every conclusion has to be stated neatly and clearly. Presentation in an organized manner can give a further push to your grades.
5. What is the theorem of Chapter 8 quadrilateral?
Theorem 8.2 can be stated as given below : If a quadrilateral is a parallelogram, then each pair of its opposite sides is equal. So its converse is : Theorem 8.3 : If each pair of opposite sides of a quadrilateral is equal, then it is a parallelogram.
6. What is the formula of quadrilateral ABCD?
The area of the quadrilateral ABCD = Sum of areas of ΔBCD and ΔABD. Thus, the area of the quadrilateral ABCD = (1/2) × d × h1 + (1/2) × d × h2 = (1/2) × d × (h2 + h2 ).
7 What is the importance of NCERT quadrilaterals class 9?
This chapter is crucial for understanding the properties and types of quadrilaterals, including parallelograms, rectangles, and squares.
8. What key properties of parallelograms should I focus on in NCERT quadrilaterals class 9?
Focus on properties such as opposite sides being equal and parallel, opposite angles being equal, and diagonals bisecting each other.
9. How many questions from maths quadrilateral class 9 were asked in previous year exams?
Questions from Chapter 8 - Quadrilaterals in Class 9 Maths might range from 2-4 questions, including both short and long answer types.
10. What is the Midpoint Theorem and its application quadrilaterals class 9 NCERT solutions?
The Midpoint Theorem states that the line segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length. It is used to solve problems related to quadrilaterals.
11. How can Vedantu's solutions help in quadrilaterals class 9 NCERT solutions?
Vedantu provides step-by-step explanations and detailed solutions to help students understand and solve problems effectively.
12. How do I prove that a given quadrilateral is a parallelogram in NCERT quadrilaterals class 9?
Use properties such as opposite sides being equal and parallel or diagonals bisecting each other to prove a quadrilateral is a parallelogram.
13. What are the conditions for a quadrilateral to be a parallelogram in class 9 quadrilaterals?
Conditions include both pairs of opposite sides being equal and parallel, and both pairs of opposite angles being equal.
14. What should I focus on while studying chapter 8 class 9 maths?
Focus on understanding the properties, theorems, and their applications in solving geometric problems.
15. How many types of quadrilaterals are there, and what are they?
Key types include parallelograms, rectangles, squares, rhombuses, and trapezoids. Each type has its unique properties and applications.


 Watch Video
Watch Video