NCERT Solutions for Maths Class 9 Coordinate Geometry Chapter 3 - FREE PDF Download
NCERT Solutions for Class 9 Mathematics introduces you to a new realm of concepts, theorems, applications, and problem-solving procedures. Coordinate Geometry class 9 concentrates on the basics of coordinate geometry. Here, you will learn about coordinate axes and how to plot a point using Cartesian Coordinates. To understand more about the principles and their applications, you must first read the full chapter and then complete all of the activities. You would need NCERT Answers for class 9 maths chapter 3 for this. This answer was produced by Vedantu's best Mathematics teachers. We've also supplied it in PDF format.
- 5.1Exercise 3.1
- 5.2Exercise 3.2
Glance on Class 9 Maths Chapter 3 - Coordinate Geometry
The coordinate plane is a flat surface where a horizontal line (x-axis) and a vertical line (y-axis) intersect at a right angle, forming a grid system known as the Cartesian Plane or Coordinate Plane.
The axes divide the plane into four sections called quadrants, which are numbered I, II, III, and IV in an anti-clockwise direction starting from the positive x-axis.
Coordinates identify each point on a plane using an ordered pair of numbers (x, y). The x-coordinate, or abscissa, indicates the horizontal distance from the y-axis, while the y-coordinate, or ordinate, shows the vertical distance from the x-axis.
To plot a point's coordinates (x, y) on a graph, start at the origin (where the axes intersect), move x units to the right if x is positive or to the left if x is negative, and then move y units up if y is positive or down if y is negative.
The signs of the coordinates tell you in which quadrant the point lies.
Both positive (x, y) - Quadrant I
Negative x, positive y - Quadrant II
Both negative (x, y) - Quadrant III
Positive x, negative y - Quadrant IV
This article contains chapter notes, important questions, exemplar solutions, exercises, and video links for Chapter 3 - Coordinate Geometry, which you can download as PDFs.
There are two exercises (4 fully solved questions) in class 9th maths chapter 3 Coordinate Geometry.
Access Exercise wise NCERT Solutions for Chapter 3 Maths Class 9
Vedantu Learning Centre, 2nd Floor, Ugra Tara Complex, Club Rd, opposite Grand Mall, Mahammadpur Kazi, Mithanpura, Muzaffarpur, Bihar 842002
Vedantu Learning Centre, Plot No. Y - 217, Plot No 4617, 2nd Ave, Y Block, Anna Nagar, Chennai, Tamil Nadu 600040
Vedantu Learning Centre, 3rd Floor, ASV Crown Plaza, No.391, Velachery - Tambaram Main Rd, Velachery, Chennai, Tamil Nadu 600042
Shree Gugans School CBSE, 54/5, School road, Selaiyur, Tambaram, Chennai, Tamil Nadu 600073
Vedantu Learning Centre, Ayyappa Enterprises - No: 308 / A CTH Road Avadi, Chennai - 600054
Sri Venkateshwara Pre-University College, NH 7, Vidyanagar, Bengaluru International Airport Road, Bengaluru, Karnataka 562157
Exercise 3.1: This exercise introduces the fundamental concepts of coordinate geometry and aims to familiarise students with terms like the Cartesian plane, coordinates of points, quadrants, distance formula, and section formula. Additionally, students learn how to find the midpoint of a line segment and the area of a triangle.
Exercise 3.2: This exercise explores different forms of equations of a straight line. Students are expected to find the equation of a straight line that passes through two given points. They will also learn how to find the slope and intercept of a line, and how to write the equation of a line in different forms such as slope-intercept form, point-slope form, and general form.
Access NCERT Solutions for Class 9 Maths Chapter 3 – Coordinate Geometry
Exercise 3.1
1. How will you describe the position of a table lamp on your study table to another person?
Ans: Consider the figure of a study stable given below, on which a study lamp is placed.
Consider the table as the rectangular plane and the lamp as a point. This table has a short edge and a long edge.
We can see that the distance of the lamp from the shorter edge is $15\ \text{cm}$ and from the longer edge, its $25\ \text{cm}$.
Therefore, depending on the order of the axes, we can conclude that the position of the lamp on the table can be described as $\left( 15,25 \right)$ or $\left( 25,15 \right)$.
2. (Street Plan): A city has two main roads which cross each other at the center of the city. These two roads are along the North-South direction and East-West direction.
All the other streets of the city run parallel to these roads and are \[200\text{ }m\] apart. There are $5$ streets in each direction. Using \[1\text{ }cm\text{ }=\text{ }200\text{ }m\] , draw a model of the city in your notebook. Represent the roads/streets by single lines. There are many cross- streets in your model. A particular cross- street is made by two streets, one running in the North–South direction and another in the East–West direction. Each cross street is referred to in the following manner: If the \[2nd\] street running in the North–South direction and 5th in the East–West direction meet at some crossing, then we will call this cross-street \[\left( 2,\text{ }5 \right)\]. Using this convention, find:
i) How many cross - streets can be referred to as \[\left( 4,\text{ }3 \right)\] .
Ans: Draw two perpendicular lines depicting the two main roads of the city that cross each other at the center.
Mark it as \[NS\] and \[EW\] .
Consider the scale as \[1\text{ }cm\text{ }=\text{ }200\text{ }m\] .
Get the Figure given below by drawing five streets that are parallel to both the main roads,
From the Figure, we can see that there is only one cross street, which can be referred as \[\left( 4,\text{ }3 \right)\].
ii) How many cross - streets can be referred to as \[\left( 3,\text{ }4 \right)\] .
Ans: From the Figure, we can see that there is only one cross street, which can be referred to as \[\left( 3,\text{ }4 \right)\] .
Exercise 3.2
1. Write the answer of each of the following questions:
i) What is the name of horizontal and the vertical lines drawn to determine the position of any point in the Cartesian plane?
Ans: X-axis is referred to as the horizontal line that is drawn to determine the position of any point in the Cartesian plane. Y-axis is the vertical line that is drawn to determine the position of any point in the Cartesian plane.
ii) What is the name of each part of the plane formed by these two lines?
Ans: Quadrant is the name of each part of the plane that is formed by x-axis and y-axis.
iii) Write the name of the point where these two lines intersect.
Ans: Origin $O$ is the point of intersection of \[x\] - axis and the $y$ - axis.
2. See the Figure, and write the following:
i) The coordinates of \[B\].
Ans: Coordinates of point \[B\] is the distance of \[B\] from $x$ - axis and \[y\] - axis.
Therefore, the coordinates of point \[B\] are \[(-5,2)\].
ii) The coordinates of \[C\].
Ans: Coordinates of point \[C\] is the distance of point \[C\] from \[x\] - axis and \[y\] -axis.
Therefore, the coordinates of point \[C\] are \[(5,-5)\].
iii) The point identified by the coordinates \[(-3,-5)\].
Ans: The point that represents the coordinates \[(-3,-5)\] is \[E\].
iv) The point identified by the coordinates \[(2,-4)\].
Ans: The point that represents the coordinates $(2,-4)$ is \[G\].
v) The abscissa of the point \[D\].
Ans: The abscissa of point \[D\] is the distance of point \[D\] from the $y$ - axis. Therefore, the abscissa of point \[D\] is $6$.
vi) The ordinate of the point \[H\].
Ans: The ordinate of point $H$ is the distance of point $H$ from the $x$ -axis. Therefore, the ordinate of point $H$ is $-3$.
vii) The coordinates of the point \[L\].
Ans: In the Figure, the coordinates of point \[L\] is the distance of point \[L\] from $x$ -axis and $y$ -axis. Therefore, the coordinates of point \[L\] are \[(0,5)\].
viii) The coordinates of the point \[M\].
Ans: In the Figure, the coordinates of point \[M\] is the distance of point \[M\] from $x$ -axis and $y$-axis. Therefore, the coordinates of point \[M\] are \[(-3,0)\].
Overview of Deleted Syllabus for CBSE Class 9 Maths Coordinate Geometry
Class 9 Maths Chapter 3: Exercises Breakdown
Conclusion
NCERT Solutions for Coordinate Geometry class 9 provides a comprehensive and detailed understanding of the fundamental concepts of coordinate geometry. This chapter introduces students to the Cartesian coordinate system and its applications in representing points and geometric shapes in a two-dimensional plane. The solutions begin by explaining the basics of coordinates, plotting points, and understanding the four quadrants of the coordinate plane. Students learn how to identify the coordinates of a point and how to plot points based on given coordinates. In previous years exams, around 2-3 questions have been asked from this chapter. NCERT Solutions for Ch 3 maths class 9 delves into the concept of the distance formula, enabling Students to calculate the distance between two points on the coordinate plane.
Other Study Material for CBSE Class 9 Maths Chapter 3
Chapter-Specific NCERT Solutions for Class 9 Maths
Given below are the chapter-wise NCERT Solutions for Class 9 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.
FAQs on NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry
1. Why should you prefer Vedantu for Maths NCERT Solutions Class 9 Chapter 3?
Vedantu is one of the most trusted education portals for the students of Class 9. The solutions of Class 9 Maths Chapter 3 developed by the expert teachers follow CBSE norms and deliver the best path for understanding the concepts of coordinate geometry well.
2. How can you prepare and complete Coordinate Geometry?
Pay attention to all the classes. Listen to the explanation given by the class teacher. Understand the concepts and solve the exercises. Refer to the NCERT Solutions Class 9 Maths Chapter 3 to clear your doubts.
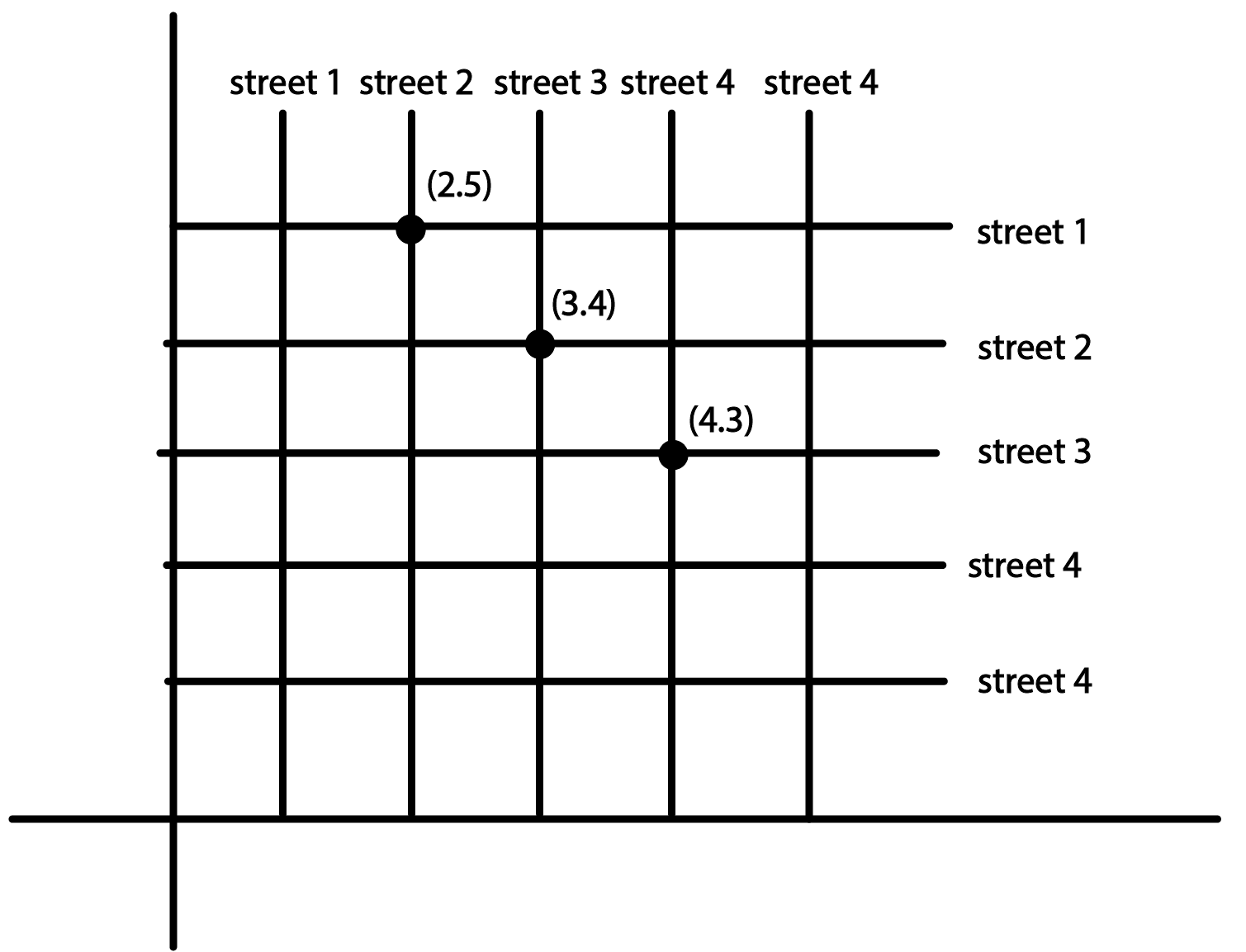
3. How can you define the position of an object on a floor?
If you use the Chapter 3 Maths Class 9 NCERT Solutions, you can will learn to define the position of an object on the floor by considering two adjacent walls as two coordinate axes.
4. Which is the best solution for NCERT Class 9 Maths?
The best solutions that are available for Class 9 Maths are the NCERT Solutions Class 9 Maths available on Vedantu. These solutions are special because they have in-depth explanations of all concepts from the full solutions of exercises to miscellaneous questions. If you practise all the chapters from these NCERT Solutions PDFs, you will get a clearer idea of what can be asked from each section. These solutions are prepared by subject matter experts, so they are 100% reliable and to the point. They are based on the latest CBSE guidelines and exam patterns.
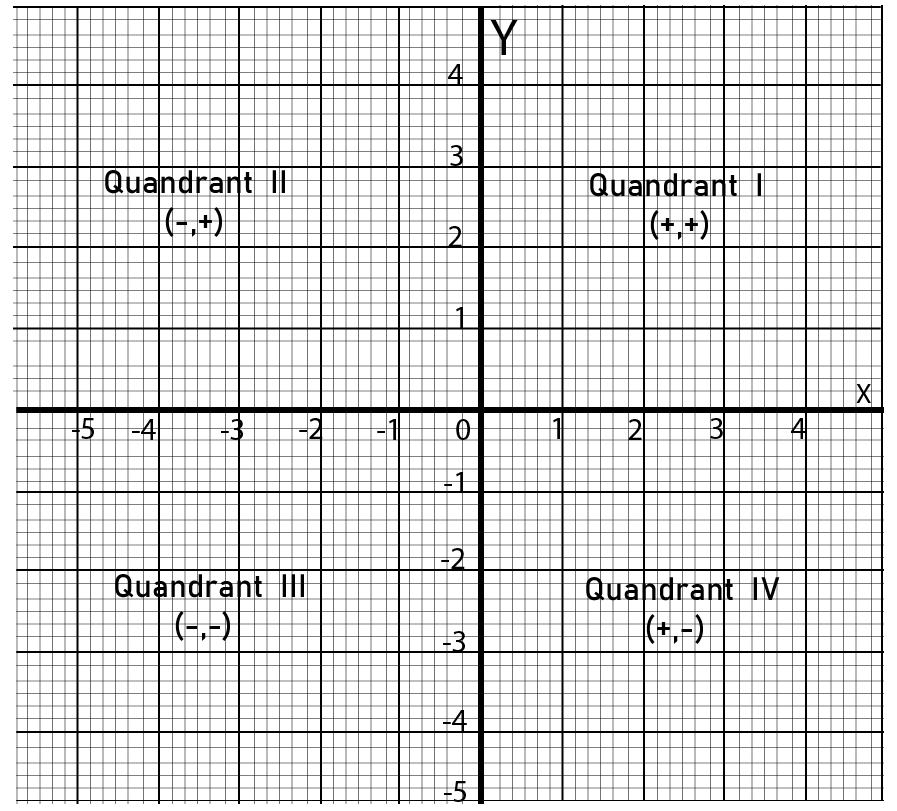
5. What are the signs of the coordinates in the four quadrants of a cartesian plane?
The signs of the coordinates in the four quadrants of a cartesian plane are - (+,+) in the first quadrant of a cartesian plane, (-, +) in the second quadrant of a cartesian plane, (-, -) in the third quadrant of a cartesian plane, and (+, -) in the fourth quadrant of a cartesian plane. + stands for positive coordinate point while - stands for a negative coordinate point. All the coordinate points in the different quadrants make up a coordinate plane
6. Are (5,0) and (0,5) ordered pairs in Class 9 Maths Chapter 3?
On plotting the above coordinates along the x-axis and the y-axis, we find that the positions of both pairs differ. (5,0) is differently placed on the Cartesian plane than (0,5). We know that when the values of both the pairs are the same but interchanged them, the position on the graph varies; we call these pairs ordered pairs. And clearly, (0,5) and (5,0) are ordered pairs because by interchanging them, their positions vary.
7. Is Class 9 Maths Chapter 3 easy?
Sure, Class 9 Mathematics Chapter 3 is simple if you put out the necessary effort and create a study plan for yourself. Vedantu is the ideal partner for you to conquer your phobia of Class 9 Mathematics Chapter 3 Coordinate Geometry. You may obtain entire solutions to the exercises by downloading the NCERT Solutions for Class 9 Maths Chapter 3 Coordinate Geometry. Vedantu even provides study programmes to assist you in organising your studies. These solutions are freely available on Vedantu's website (vedantu.com) and mobile app.
8. What is the Cartesian coordinate system in class 9 chapter 3 maths?
In class 9 chapter 3 maths the cartesian coordinate system uses two perpendicular lines, the x-axis and the y-axis, to define points on a plane. The intersection of these axes is called the origin. Each point is represented by an ordered pair (x, y), indicating its distance from the axes.
9. How do you find the distance between two points in coordinate geometry?
In class 9 maths chapter 3 solutions, to find the distance between two points, imagine a straight line connecting them. Measure the length of this line, considering their x and y coordinates. This process involves a specific calculation, often visualized as forming a right triangle.
10. What is the section formula in coordinate geometry in class 9th maths chapter 3?
In coordinate geometry class 9 the section formula helps to find the coordinates of a point that divides a line segment into a given ratio. It involves using the coordinates of the endpoints and the specified ratio. This is useful in locating a precise point along the segment.