NCERT Solutions for Class 10 Maths Chapter 7 Coordinate Geometry - Free PDF Download






NCERT Solutions for Class 10 Chapter 7 Coordinate Geometry

 Share
Share


























FAQs on NCERT Solutions for Class 10 Chapter 7 Coordinate Geometry
1. How to find the circumcentre of a triangle by the section formula?
Circumcentre is defined as the point of intersection of the perpendicular bisectors of the sides of a triangle.
The coordinates of circumcentre of triangle is calculated whose coordinates of vertices are given, by the application of section formula i.e., midpoint formula. The following steps are involved for calculating the coordinates of circumcentre:
Step1: Using the midpoint formula, find the coordinates of midpoint (xm, ym), of each side AB, BC and AC.
Step2: Calculate the slope of each side. If the slope of any side is ‘m1’ then, the slope of line perpendicular to it will be 1/m1. Assume, m = 1/m1.
Step3: Using coordinates of midpoint (xm,ym), and the slope of perpendicular line i.e., ‘m’. write the equation of line (y-ym) = m (x-xm).
Step4: Similarly, find the equation of other lines.
Step5: Solve them to find out their intersection point.
The obtained intersection point will be the circumcentre of the given triangle.
2. What will be the equation of straight line having 2-unit distance from the origin and passing through the point (4, -2)?
Let the equation of straight line be given as ax + by + c = 0.
The perpendicular distance from any point is given by formula: | ax+by+c / √(a²+b²) |
Given that, the straight line is having 2-unit distance from origin (0,0).
So, | a(0)+b(0)+c / √(a²+b²) | = 2
⇒ | c / √(a²+b²) | = 2
⇒ c = ± 2√(a²+b²)
Assume, value of c = - 2√(a²+b²) …..(1)
Also, the straight line passes through the point (4, -2). Putting the coordinates of given point in the equation of straight line, we get:
4a – 2b + c = 0
Replacing the value of ‘c’ from equation (1), we get:
4a – 2b - 2√(a²+b²) = 0
⇒ 4a – 2b = 2√(a²+b²)
Square both sides of above equation,
(4a – 2b)2 = (2√(a²+b²)2
⇒ 16a2 + 4b2 – 16ab = 4(a²+b²) (cancel out ‘4b2’ on both sides)
⇒ 12a2 = 16ab (cancel out ‘a’ on both sides)
⇒ 3a = 4b
⇒ b = 3a/4 …..(2)
Put the value of ‘b’ obtained in equation (1) to get the value ‘c’ in terms of ‘a’.
c = - 2√(a²+b²)
⇒ c = - 2√(a²+9(a)² / 16) = -2√[25(a)² / 16]
⇒ c = -(5/2 a) …..(3)
Now, put the values of ‘b’ and ‘c’ from equation (2) and equation (3) respectively in the assumed equation of straight line i.e., ax + by + c = 0.
ax + (3a/4)y - (5/2 a) = 0. (where, a ≠ 0, ‘a’ can be any arbitrary number except 0)
Let us assume the value of ‘a’ = 4. Then,
Required equation of straight line will be: 4x + 3y - 10 = 0
3. How is the area of a triangle formed by three points is expressed in Coordinate Geometry?
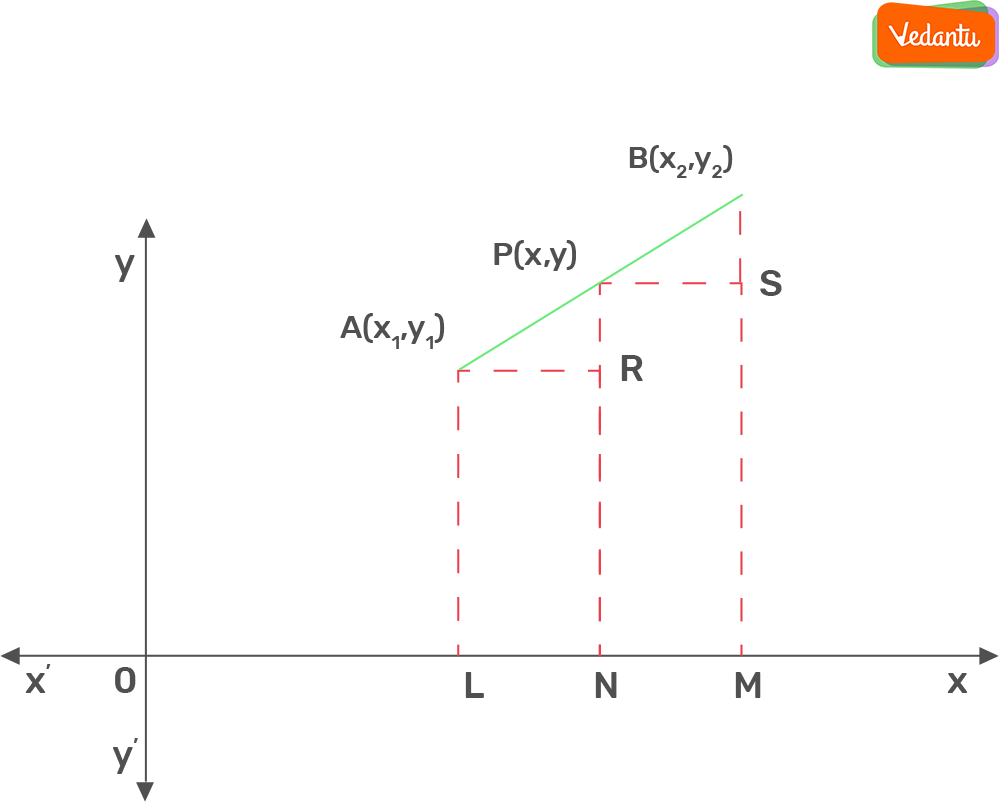
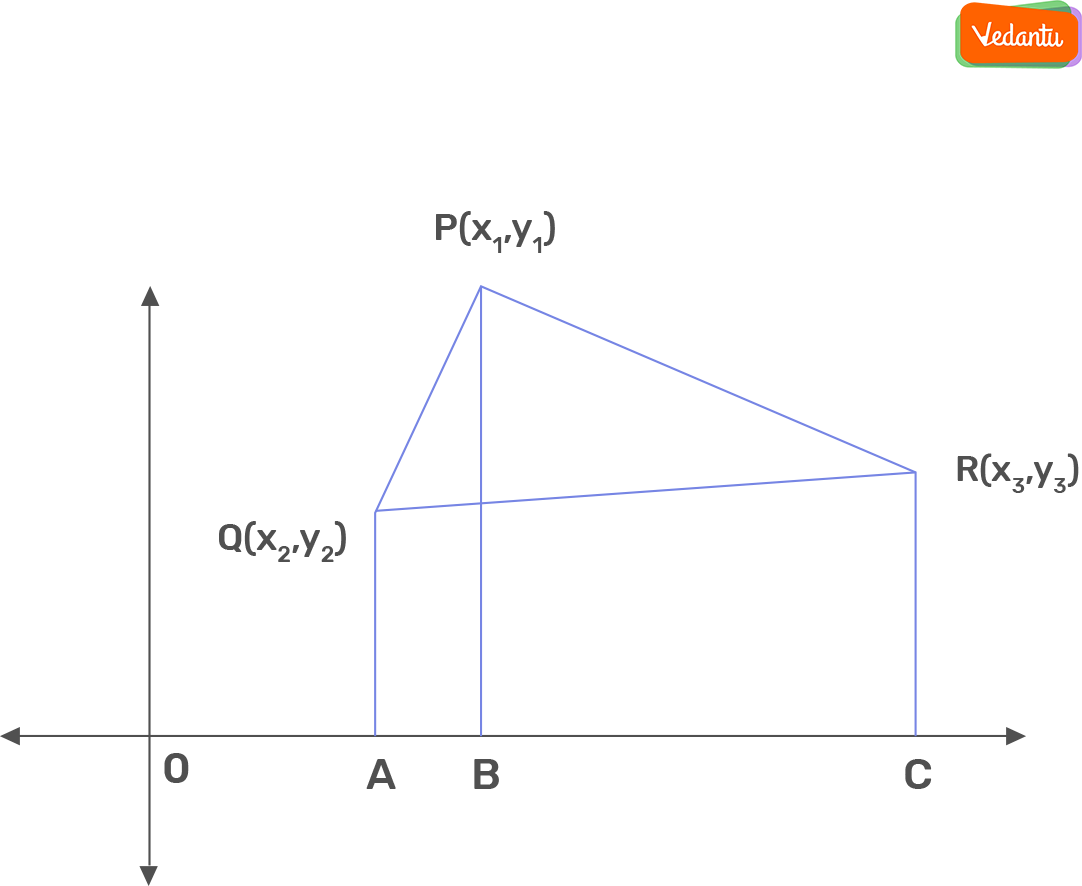
Let ABC be a triangle whose vertices are A (x1, y1), B (x2, y2) and C (x3, y3).
Draw AP, BQ and CR perpendiculars from vertices A, B and C, respectively, to the x-axis. Clearly ABQP, APRC and BQRC are all trapezium.
From above figure,
Area of Δ ABC = Area of trapezium ABQP + Area of trapezium APRC – Area of trapezium BQRC
We know that the area of trapezium = 1/2 (sum of parallel sides) (distance between them)
Therefore, area of Δ ABC = 1/2 (BQ + AP) QP + 1/2 (AP + CR) PR – 1/2 (BQ + CR) QR
= 1/2 (y2 + y1) (x1 – x2) + 1/2 (y1 + y3) (x3 – x1) – 1/2 (y2 + y3) (x3 – x2)
= 1/2 [x1(y2 -y3) + x2(y3 -y1) + x3(y1 – y2)]
Thus, the area of a triangle formed by three points in coordinate geometry is numerical value of expression: 1/2 |[x1(y2 -y3) + x2(y3 -y1) + x3(y1 – y2)]|.
4. What are some real-world applications for Coordinate Geometry?
Coordinate Geometry is used in navigation systems, computer graphics, and even designing buildings!
5. What are the concepts covered in ch7 Class 7 Maths Coordinate Geometry?
Ch7 Class 10 Maths coordinate geometry includes an introduction to coordinate geometry. Coordinate Geometry is the branch of mathematics that helps us to exactly locate a given point with the help of an ordered pair of numbers. Coordinate geometry is also known as cartesian geometry. Coordinate geometry class 10 covers the concepts of how to find the distance between two points whose coordinates are given. Find the coordinates of the point which divides the line segment joining two given points in the given ratio. Finally students will learn how to find the area of a triangle in terms of the coordinate of its vertices.
6. What is called a Coordinate Plane?
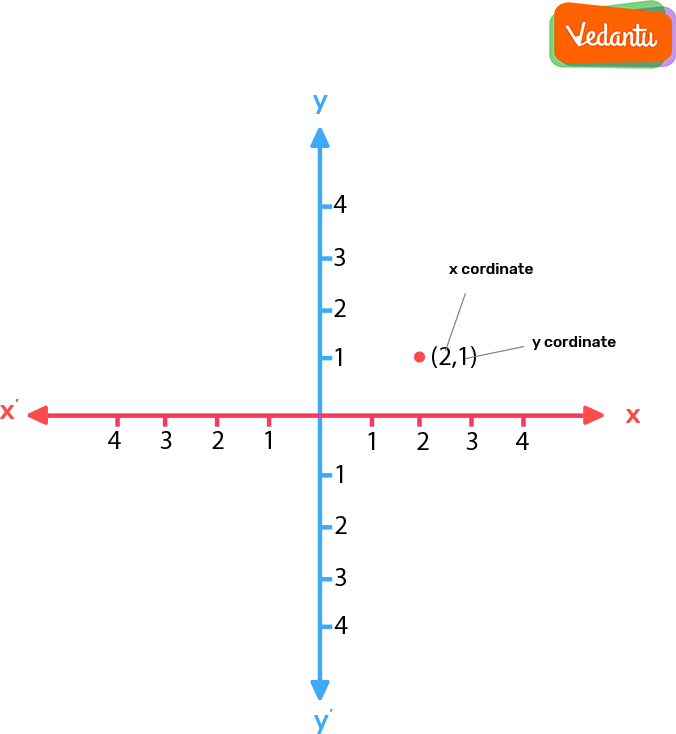
A two-dimensional plane that is formed by the intersection of one horizontal line called the x-axis and one vertical line called the y-axis. These lines are perpendicular to each other and intersect at a point O called the Origin. This axis divides the plane into four parts called quadrants. This plane is called the coordinate plane or XY- plane. The coordinate plane is also called the Cartesian plane. And the axis is called the coordinate axis.

7. Why do we need Coordinate Geometry?
Coordinate geometry has various applications in our day to daily life. Some of the areas where coordinate geometry is used are given as follow:
In computers, mobile phones, etc. to locate the position of cursor or any finger touch.
To determine the exact location of an airplane, trains etc while moving.
In GPS locations in digital maps to point the exact locations.
Coordinate geometry is also used in constructions of roads, buildings, etc.
Coordinate geometry is also used in visualizing 2D and 3D objects in the cartesian plane.
8. How do I plan my study for Class 10 exams?
To study and score well in Class 10 CBSE exams, students need to develop an effective strategy that will help them cover the syllabus. Here are some tips to plan your studies well in advance;
Go through the complete syllabus
Go through the unit-wise weightage of each chapter. You can find it here.
Make a list of important formulas from each chapter
Make sure to practice well all the exercise questions
Revise the concepts well before the exams
9. What are the most important formulas that I need to remember in Chapter 7 Coordinate Geometry of Class 10 Maths?
Chapter 7 of NCERT Class 10 Maths is Coordinate Geometry. Students should remember the following important formulas from this chapter -
The distance formula
The section formula
Area of a triangle using coordinates
The midpoint of a line segment joining two points
Distance of a point from the origin
Students should practice the examples given in the chapter and the exercise questions at the end to understand the concepts clearly and to score well in exams.
These solutions are available on Vedantu's official website(vedantu.com) and mobile app free of cost.
10. Where can I find the solutions to Chapter 7 Coordinate Geometry of Class 10 Maths?
Students can find the solutions to all exercise questions of NCERT Class 10 Maths from Vedantu’s website. The solutions are curated by subject experts to make the studies easier for students :
Go to Vedantu.
Here you will see all the chapters listed on the page.
Click on the chapter for which you want the solutions.
The solutions will appear on the screen.
You can also download the solutions for all the chapters by clicking on ‘Download PDF’. These can be viewed offline too.
11. Are there any negative coordinates in Coordinate Geometry?
Yes! Points can lie to the left (negative x) or below (negative y) of the origin (0,0) on the coordinate plane.
12. How many exercises are there in Chapter 7 of Coordinate Geometry of Class 10 Maths?
There are a total of four exercises. To understand how to solve them easily, you can visit Vedantu to avail the NCERT Solutions curated by experts. That’s not all, right from important questions to revision notes, you will find several tools to help you become thorough in this chapter.


 Watch Video
Watch Video